Árbol filogenético

Introducción teórica en Filogenia.

Un árbol filogenético es un esquema arborescente que muestra las relaciones evolutivas entre varias especies u otras entidades que se cree que tienen una ascendencia común.

Árboles filogenéticos en biología

A diferencia de los árboles genealógicos, en los que se utiliza información proporcionada por los familiares, para los árboles filogenéticos se usa información proveniente de fósiles y de la comparación anatómica, fisiológica y molecular de los organismos actuales.

Tanto los árboles genealógicos como los filogenéticos tienen un tronco y ramas, pero en los últimos se muestran las relaciones entre especies y no entre individuos.

Los árboles filogenéticos se construyen tomando en cuenta la evolución biológica, basándose en la evidencia de que todos los organismos son descendientes de un ancestro común. Así, todos los organismos, ya sean vivos o extintos, se encuentran emparentados en algún grado. En ocasiones se denomina «árbol de la vida» al árbol filogenético que engloba a todos los seres vivos, pasados y presentes.

Tipos de árboles filogenéticos

Fig. 3: Árbol sin raíz de la familia Miosina.^[1]

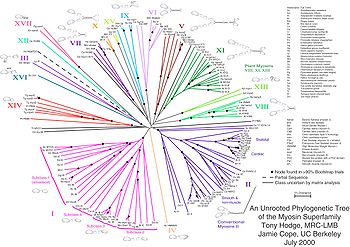
Un árbol filogenético enraizado es un árbol directo, con un único nódulo que corresponde al ancestro común más reciente de todas las entidades de las hojas del árbol. La figura 1 muestra un árbol filogenético enraizado coloreado de acuerdo con el «sistema de tres dominios». Los árboles genéticos sin raíz ilustran la relación de los nódulos de las hojas sin hacer asunciones sobre ascendencia. Mientras que los árboles sin raíz siempre pueden ser generados a partir de árboles enraizados omitiendo la raíz, una raíz no puede ser inferida a partir de un árbol sin raíz sin algunos medios para identificar la ascendencia. Esto suele hacerse incluyendo un grupo externo en los datos entrantes o introduciendo asunciones adicionales sobre las tasas relativas de evolución en cada rama, como una aplicación de la hipótesis del reloj molecular. La figura 2 muestra un árbol filogenético sin raíz^[2] para la miosina, una familia genética de proteínas.

Un dendrograma es un término genérico para la representación diagramática de un árbol filogenético.

Un cladograma es un árbol formado usando métodos cladísticos. Este tipo de árbol sólo representa un patrón de ramificación, es decir, que la longitud de sus ramas no representan el tiempo.

Un filograma es un árbol filogenético que representa explícitamente un número de cambios de rasgos de carácter a lo largo de la longitud de sus ramas; es el resultado de la aplicación de los principios de la sistemática evolutiva (relaciones de parentesco inferidas).

Un fenograma es un dendrograma no enraizado en que se establecen las relaciones de parentesco fenético de los organismos estudiados; surgen de la aplicación de los métodos de la taxonomía numérica.

Un cronograma es un árbol filogenético que representa explícitamente el tiempo evolutivo proporcionalmente a la longitud de sus ramas.

Cladística y caracteres

Artículo principal: Cladística

La mejora de los métodos computacionales para el tratamiento de la información ha introducido un número interesante de algorítmicos cladísticos para la clasificación mediante árboles filogenéticos. Muchos de esos árboles consideran un conjunto de especies representadas por un conjunto de caracteres. Un carácter es cualquier característica bien definida de la especie que permita dividir el conjunto de especies en grupos, según el valor que toma el carácter para cada especie. Así un subconjunto de las especies formará un grupo respecto a dicho carácter si comparten una misma forma o valor de dicho carácter.

Cada carácter permite construir un árbol filogenético cladístico que satisface ciertas propiedades razonables. Los algoritmos usuales pueden construir para un conjunto de especies numerosos árboles filogenéticos, y extraer de entre ellos alguno que sea óptimo en algún sentido. Si las condiciones de optimidad están bien escogidas esos algoritmos permiten encontrar el verdadero árbol filogenético para un grupo de especies relacionables.

Árbol filogenético en lingüística

En lingüística histórica también ha sido común el uso de árboles filogenéticos para clasificar las lenguas descendientes de una lengua madre común o protolengua. Su uso empezó en el siglo XIX cuando el uso extensivo de varias metáforas biológicas aplicadas a la evolución y diversificación de las lenguas humanas y la aparición del método comparativo llevó al intento de dibujar árboles genealógicos para las familias de lenguas.

Modernamente la construcción de árboles filogenéticos se basa en el análisis cladístico aplicado, bien al léxico (considerando que dos lenguas comparten alguna característica cuando mantienen ambas cierta forma léxica concreta), o bien a características fonológicas o gramaticales.

Sin embargo, la representación de las familias de lenguas mediante árboles filogenéticos tiene limitaciones cuando se aplica a ciertas familias, ya que las lenguas, a diferencia de los individuos biológicos, no tienen características permanentes por la influencia mutua, el sprachbund o convergencia común por factores sociales. La construcción de árboles filogenéticos resulta más sencilla para unas familias lingüísticas que para otras, por ejemplo, para las lenguas austronesias, cuya expansión por el pacífico se produjo saltando de isla en isla, la construcción de árboles resulta más sencilla que para las lenguas urálicas o altaicas en las que las influencias de unas lenguas en otras y la presencia de préstamo gramatical dificulta enormemente la elaboración de árboles filogenéticos.

Árboles cladísticos como modelos de cambio

Árboles filogenéticamente perfectos

Una condición importante en los árboles empleados en lingüística es la condición de filogenia perfecta. Los árboles que satisfacen dicha condición son los árboles filogenéticamente perfectos, que satisfacen la siguiente definición:

Un árbol $\scriptstyle T$ para un conjunto de lenguas $\scriptstyle {\mathcal {L}}$ tiene filogenia perfecta si para un conjunto de caracteres $\scriptstyle C$ , si es posible etiquetar los nodos del árbol de tal manera que los caracteres evolucionen a lo largo del árbol sin retromutaciones o evolución paralela en $\scriptstyle T$ . En este caso se dice que $\scriptstyle T$ es compatible con los valores observados en las "hojas" (nodos extremos) para todos los caracteres.

Cuando un nodo o proto-lengua B que no posee una característica que sí posee algún otro nodo o proto-lengua A de la que deriva, experimenta un cambio o mutación dando lugar a una proto-lengua C que vuelve a poseer la característica presente en la proto-lengua A y ausente en la proto-lengua B.

Redes filogenéticas

Es bien conocido, que los árboles filogenéticos no pueden representar adecuadamente situaciones de evolución lingüística si hay un contacto lingüístico importante entre las ramas del árbol. En la medida que el préstamo lingüístico entre ramas puede ser claramente identificado, pueden ignorarse las características prestadas y seguir usándose árboles. Sin embargo, en los casos en que la historia pasada no es bien conocida y los rasgos heredados no pueden ser separados de los rasgos prestados pueden introducirse las llamadas redes filogenéticas, que en esencia son una generalización de los árboles filogenéticos (de hecho un árbol filogenético es un tipo muy particular de red filogenética).^[3]

Una red filogenética es un objeto topológico etiquetado cuya topología no es estrictamente un árbol, sino un árbol al que se añaden líneas adicionales entre nodos de ramificación para representar situaciones de contacto o préstamo lingüístico. Estas líneas adicionales hacen que una red filogenética usa grafos que topológicamente pueden contener ciclos y, por tanto, no necesariamente son árboles topológicos. En una red filogenética se consideran todos los subárboles posibles, siendo filogenéticamente adecuados si la evolución temporal de cualquier carácter puede ser representado por un árbol filogenético contenido en la red.

Véase también

Referencias

↑ Hodge, T. & M. J. T. V. Cope. 2000. A Myosin Family Tree. Journal of Cell Science 113: 3353-3354.
↑ Maher, B. A. 2002. Uprooting the Tree of Life. The Scientist 16: 18 (Sep. 16, 2002); subscription only Archivado el 2 de octubre de 2003 en Wayback Machine.
↑ Warnow, Evans, Ringe y Nakhleh: "Stocastic Models of Language Evolution and an Application to the Indo-European Family of Languages"

Imágenes

General

Datos: Q242125
Multimedia: Phylogenetic tree of life / Q242125

[1] Hodge, T. & M. J. T. V. Cope. 2000. A Myosin Family Tree. Journal of Cell Science 113: 3353-3354.

[2] Maher, B. A. 2002. Uprooting the Tree of Life. The Scientist 16: 18 (Sep. 16, 2002); subscription only Archivado el 2 de octubre de 2003 en Wayback Machine.

[3] Warnow, Evans, Ringe y Nakhleh: "Stocastic Models of Language Evolution and an Application to the Indo-European Family of Languages"

[1]

[2]

[3]