Ir al contenido

Archivo:Abu Reyhan Biruni-Earth Circumference.svg

Contenido de la página no disponible en otros idiomas.
De Wikipedia, la enciclopedia libre

Ver la imagen en su resolución original ((Imagen SVG, nominalmente 1000 × 900 pixels, tamaño de archivo: 16 kB))

Este es un archivo de Wikimedia Commons, un depósito de contenido libre hospedado por la Fundación Wikimedia. Más abajo se reproduce su página de descripción con la información sobre su origen y licencia.

Resumen

Descripción
English: Biruni (973 - 1048) developed a new method using trigonometric calculations to compute earth's radius and circumference based on the angle between the horizontal line and true horizon from a mountain top with known height. He calculated the height of the mountain by going to two points at sea level with a known distance apart and then measuring the angle between the plain and the top of the mountain for both points.

Biruni's estimate of 6,339.9 km for the Earth radius had an error of 0.0026 and was 16.8 km less than the current value of 6,356.7 km. The idea came to him when he was on top of a tall mountain near Nandana in Pakistan. He measured the dip angle using an astrolabe and he applied to the law of sines formula. He also made use of algebra in his calculation.

  • A = Highest point of mountain
  • B = Lowest point of mountain
  • h = Height of the mountain
  • C = Lowest point of true horizon visible from point A
  • O = Centre of Earth
  • α = Dip angle
  • r = Earth's radius

Solution:
The angle AOC = α.
AO=(r+h) is the hypotenuse in triangle AOC.
r=(r+h)·cos(α)
Then the right side can be simplified to find r.

r=h·cos(α)/(1-cos(α))


Français : Biruni (973-1048) développa une nouvelle méthode utilisant la trigonométrie pour calculer le rayon et la ciconférence de la Terre, basée sur l'angle entre la ligne horizontale et l'horizon réel depuis le sommet d'une montagne de hauteur connue. Il calcula la hauteur de la montagne en se rendant en deux points situés au niveau de la mer dont l'écartement était connu, puis en mesurant l'angle entre la ligne horizontale formée par les deux points au niveau de la mer et le sommet de la montagne, et ceci depuis chacun des deux points.

L'estimation de Biruni de 6 339,9 km pour le rayon de la Terre comportait une erreur de 0,26 %, soit une valeur inférieure de 16,8 km par rapport à la valeur actuelle de 6 356,7 km. L'idée lui était venue alors qu'il se trouvait au sommet d'une haute montagne, près de Nandana en Inde. Il mesura l'angle d'incinaison avec un astrolabe et il appliqua la formule des sinus. Il fit également usage de l'algèbre pour ses calculs.

  • A = point culminant de la montagne
  • B = point le plus bas de la montagne
  • h = hauteur de la montagne
  • C = point le plus bas de l'horizon vrai visible du point A
  • O = Centre de la Terre
  • α = angle d'inclinaison
  • r = rayon de la Terre

Solution :
L'angle AOC = α.
AO=(r+h) est l'hypothénuse du triangle AOC.
r=(r+h)·cos(α)
Puis le côté droit se simplifie pour trouver r.

r=h·cos(α)/(1-cos(α))
Fecha
Fuente Trabajo propio Using Geogebra and Inkscape
Autor Nevit Dilmen
SVG desarrollo
InfoField
 
El código fuente de esta imagen SVG es válido.
 
Esta geometría fue creada con Inkscape.
 
y con GeoGebra.
 
 This geometry uses embedded text that can be easily translated using a text editor.

Licencia

Yo, el titular de los derechos de autor de esta obra, la publico en los términos de la siguiente licencia:
w:es:Creative Commons
atribución compartir igual
Este archivo se encuentra bajo la licencia Creative Commons Genérica de Atribución/Compartir-Igual 3.0.
Eres libre:
  • de compartir – de copiar, distribuir y transmitir el trabajo
  • de remezclar – de adaptar el trabajo
Bajo las siguientes condiciones:
  • atribución – Debes otorgar el crédito correspondiente, proporcionar un enlace a la licencia e indicar si realizaste algún cambio. Puedes hacerlo de cualquier manera razonable pero no de manera que sugiera que el licenciante te respalda a ti o al uso que hagas del trabajo.
  • compartir igual – En caso de mezclar, transformar o modificar este trabajo, deberás distribuir el trabajo resultante bajo la misma licencia o una compatible como el original.

Leyendas

Añade una explicación corta acerca de lo que representa este archivo

Elementos representados en este archivo

representa a

tipo de archivo

image/svg+xml

suma de verificación

4dd53114d5cd203e9b0011067229c31d0c5ea202

método de determinación: SHA-1

altura

900 píxel

ancho

1000 píxel

Historial del archivo

Haz clic sobre una fecha y hora para ver el archivo tal como apareció en ese momento.

Fecha y horaMiniaturaDimensionesUsuarioComentario
actual05:25 2 may 2010Miniatura de la versión del 05:25 2 may 20101000 × 900 (16 kB)NevitCrop
05:21 2 may 2010Miniatura de la versión del 05:21 2 may 20101390 × 1220 (16 kB)NevitYellow removed
05:19 2 may 2010Miniatura de la versión del 05:19 2 may 20101390 × 1220 (16 kB)NevitImage version
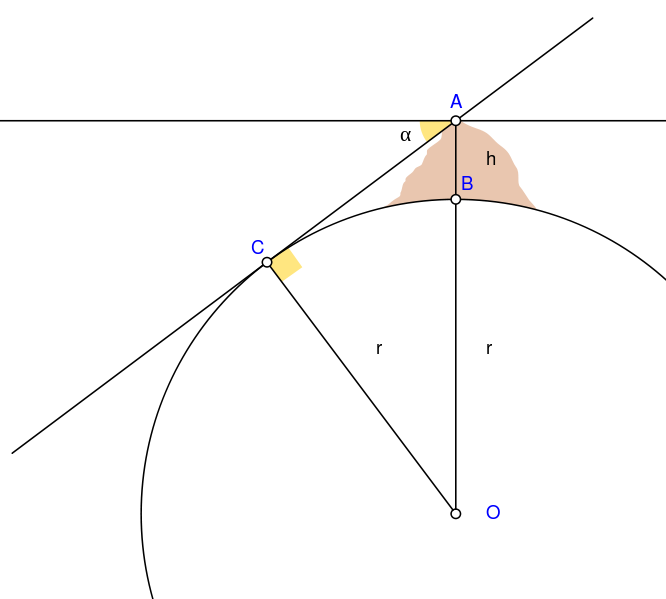
05:18 2 may 2010Miniatura de la versión del 05:18 2 may 2010640 × 480 (22 kB)Nevit{{Information |Description={{en|1=Biruni (973 - 1048) developed a new method using trigonometric calculations to compute earth's circumference based on the angle between the horizontal line and true horizon from a mountain top with known height. He calcu

Uso global del archivo

Las wikis siguientes utilizan este archivo:

Metadatos

Este archivo contiene información adicional, probablemente añadida por la cámara digital o el escáner usado para crearlo o digitalizarlo.

Si el archivo ha sido modificado desde su estado original, pueden haberse perdido algunos detalles.

Obtenido de «https://es.wikipedia.org/wiki/Archivo:Abu_Reyhan_Biruni-Earth_Circumference.svg»