Raíz cuadrada

Se llama en matemáticas, la raíz cuadrada de un número x como aquel número y tal que multiplicado por sí mismo tenga como producto x. La raíz cuadrada de x se expresa ${\sqrt {x}}$ o $x^{\frac {1}{2}}$. Por ejemplo:

Representación de "raíz cuadrada de x".

${\sqrt {16}}=4$, ya que $4^{2}=4\times 4=16$

${\sqrt {2}}=1,4142135623730950488...$

Las raíces cuadradas fueron uno de los primeros desarrollos de las matemáticas, siendo particularmente investigadas durante el periodo pitagórico, cuando el descubrimiento de que raíz de 2 era irracional (inconmensurable) o no expresable como cociente alguno supuso un hito en la matemática de la época.

Posteriormente se fue ampliando la definición de raíz cuadrada. Para los números reales negativos, la generalización de la función raíz cuadrada de éstos da lugar al concepto de los números imaginarios y al cuerpo de los números complejos, algo necesario para que cualquier polinomio tenga sus raíces todas sus raíces (teorema fundamental del álgebra). La diagonalización de matrices también permite el cálculo rápido de la raíz de una matriz.

Inicialmente mostraron su utilidad para la resolución de problemas trigonométricos y geométricos como la diagonal de un cuadrado o el teorema de Pitágoras. Posteriormente fueron ganando utilidad para operar con polinomios y resolver ecuaciones de segundo grado o superior, siendo una de las herramientas matemáticas más elementales hoy en día.

Historia

El Papiro de Ahmes datado en 1650 a. C., que copia textos más antiguos, muestra cómo los egipcios extraían raíces cuadradas.​

En la antigua India, el conocimiento de aspectos teóricos y aplicados del cuadrado y la raíz cuadrada fue al menos tan antiguo como los Sulba Sutras, fechados alrededor del 800-500 a. C. (posiblemente mucho antes). Un método para encontrar muy buenas aproximaciones a las raíces cuadradas de 2 y 3 es dado en el Baudhayana Sulba Sutra.​ Aryabhata en su tratado Aryabhatiya (sección 2.4), dio un método para encontrar la raíz cuadrada de números con varios dígitos.

David Eugene Smith en History of Mathematics, dice, acerca de la situación existente: "En Europa esos métodos (para encontrar el cuadrado y la raíz cuadrada) no aparecieron antes de Cataneo (1546). Él dio el método de Aryabhata para determinar la raíz cuadrada".​

El símbolo de la raíz cuadrada $({\sqrt {\ }})$ fue introducido en 1525 por el matemático Christoph Rudolff para representar esta operación​​ que aparece en su libro Coss, siendo el primer tratado de álgebra escrito en alemán vulgar. El signo no es más que una forma estilizada de la letra r minúscula para hacerla más elegante, alargándola con un trazo horizontal, hasta adoptar el aspecto actual, que representa la palabra latina radix, que significa raíz. También se conjetura que pudiese haber surgido de la evolución del punto que en ocasiones se usaba anteriormente para representarlo, donde posteriormente se le habría añadido un trazo oblicuo en la dirección del radicando.

Tiempo atrás, varios matemáticos vieron la necesidad de idear números que representasen la raíz cuadrada de números negativos, para poder resolver todas las ecuaciones de segundo grado, pero no será hasta 1777 cuando Euler simbolice la raíz cuadrada de -1 con la letra i, dando así cabida al desarrollo de los números complejos.

Irracionalidad de las raíces cuadradas

Las raíces cuadradas de los números enteros que no son cuadrados perfectos son siempre números irracionales, que son números no expresables como el cociente de dos números enteros. Es decir, la raíz cuadrada de un número entero siempre será entero o irracional.

Se puede demostrar fácilmente como sigue:

• n puede ser expresado como el producto de una serie de factores primos elevados a diversos exponentes. De ser todos pares, las propiedades de la potenciación permiten reducir la raíz a un número natural. Sólo si uno o más de los factores tiene un exponente impar la raíz no es natural.
• Si ${\sqrt {n}}$ fuera racional se debería poder expresar como ${\frac {p}{q}}$ con p, q enteros y primos entre sí. Elevando al cuadrado ambas partes se obtiene que $n={\frac {p^{2}}{q^{2}}}$ lo que es absurdo, pues a un lado queda al menos un factor primo con exponente impar mientras que al otro lado de la igualdad tanto $p^{2}$ como $q^{2}$ se expresan en función de producto de primos elevados a exponentes necesariamente pares

Por una reducción al absurdo llegaron los pitagóricos a la demostración de la irracionalidad de la raíz cuadrada de 2, atribuido a Hipaso, un discípulo de Pitágoras. La idea, contraria a lo esperado en la matemática de entonces supuso una crisis en la filosofía pitagórica.

No obstante, es exactamente la longitud de la diagonal de un cuadrado cuyo lado mide 1, siendo fácil la construcción gráfica de la raíz. Por ello buena parte de la matemática helénica se centró en la geometría aplicada como forma de calcular gráficamente valores como ese. Teodoro de Cirene llegó a la espiral que lleva su nombre que permite representar gráficamente cualquier raíz y posteriormente Euclides llegó a un método más general.

Resolución de raíces cuadradas

Hoy en día existen muchos métodos para poder calcular la raíz cuadrada, habiendo algunos significativos por el hecho de ser a mano y otros por el hecho de ser calculados por una máquina.

Algoritmo manual

Cuando resolvemos la raíz cuadrada con su método de resolución usual podemos ver las partes en las que se divide, aunque las esenciales de esta no tienen por qué aparecer o ser usadas solamente en la operación para ser calculada la raíz cuadrada, según esta imagen podemos ver que las partes de las que se compone son:

1. Radical, es el símbolo que indica que es una raíz cuadrada.
2. Radicando, es el número del que se obtiene la raíz cuadrada.
3. Raíz, es propiamente la raíz cuadrada del radicando.
4. Renglones auxiliares, nos ayudaran a resolver la raíz cuadrada.
5. Resto, es el número final del proceso para resolver la raíz cuadrada.

Los pasos a seguir son estos:

Paso 1

• Paso 1: Se separa el número del radicando (en el ejemplo, 5836.369) en grupos de dos cifras. La separación se hace desde el signo de decimal (si lo hubiera) hacia la derecha y hacia la izquierda. Si del lado de los decimales (a la derecha del punto, es decir 369) no hay un número par de cifras, es evidente que quedaría una suelta: en ese caso, se le añadiría un cero. Si del lado de los enteros (a la izquierda del punto, es decir, 5836) quedara un número suelto, se quedaría así. En la imagen de la derecha podemos ver el número 5836.369 dividido en grupos de dos cifras; después del número 9 se ha agregado un cero (en azul) pues en el lado decimal no puede haber un grupo de una cifra (en el ejemplo, esta separación quedaría así: 58/36.36/90)

Paso 2

• Paso 2: Se busca un número que multiplicado por sí mismo (es decir, elevado al cuadrado) de como resultado el número que coincida o que más se aproxime por debajo al primer grupo de números de la izquierda (en el ejemplo, 58). El resultado no puede ser mayor que 58. Una vez encontrado el número se agrega a la parte de la raíz. En este caso el número sería el 7, porque 7x7 es 49. Otra posibilidad sería 6x6, pero daría 36 (lo que quedaría más alejado de 58) y 8x8, pero daría 64 (lo que excedería a 58).

Paso 3

• Paso 3: El número elegido (7) es el primer resultado de la raíz cuadrada. En el paso anterior lo escribíamos en el cajetín de la derecha. Ahora lo multiplicamos por sí mismo. El resultado (49) se escribe debajo del primer grupo de cifras de la izquierda (58), y se procede a restarlo. El resultado de la resta (58-49) es 9. Una vez obtenido el resultado de la resta, se baja el siguiente grupo de dos cifras (36), con lo que la siguiente cifra de la raíz es ahora la unión del resultado de la resta anterior con las nuevas cifras bajadas (es decir, 936).Para continuar la extracción de la raíz cuadrada multiplicamos por 2 el primer resultado (7) y lo escribimos justo debajo de éste, en el siguiente renglón auxiliar (en la imagen, el 14 está escrito justo debajo del 7, ya que 7x2 es 14).

Paso 4

• Paso 4: En este paso hay que encontrar un número n que, añadido a 14, y multiplicado por ese mismo n, de como resultado un número igual o inferior a 936. Es decir, podría ser 141x1, 142x2, 143x3... y así hasta 149x9. Muchas veces se utiliza el procedimiento de tanteo para hallar ese número, si bien se puede emplear el método de dividir las primeras dos cifras del residuo (93) entre el número del renglón auxiliar (14). La primera cifra del resultado que no sea cero, aunque sea un decimal, es, generalmente, la que buscamos. El resultado se agrega al número de la raíz y al del renglón auxiliar. En este caso 93 dividido entre 14 es 6. De manera que la operación buscada es 146x6= 876 (operación que añadimos en el renglón auxiliar). El siguiente resultado de la raíz cuadrada es 6. También procedemos a anotarlo en el radicando.

Paso 5

• Paso 5: El procedimiento a seguir es el mismo que anteriormente. El resultado de la operación anterior (876) se coloca debajo del número procedente de la resta anterior (936) y se restan. Al resultado de la resta (60) se le añade el siguiente grupo de cifras del radical (en este caso, 36). Si el siguiente grupo está después del punto decimal se agrega un punto decimal al número de la raíz. El nuevo número obtenido es 6036.

Paso 6

• Paso 6: Retomamos el procedimiento del paso 4. La cifra de la raíz (76) se multiplica por dos (resultando 152). Buscamos un número que añadido a 152 y multiplicado por ese mismo número nos dé una cantidad aproximada a 6036. Sería, por tanto, 1521x1, 1522x2, 1523x3, etc. Lo podemos hacer por tanteo, o por el procedimiento de dividir en este caso, las tres primeras cifras de la raíz por las tres primeras cifras de la línea auxiliar (nótese que antes eran las dos primeras cifras), es decir, 603/152 (el número buscado es 3, ya que el resultado es 3.9 y hemos dicho que la cifra que debemos tomar es la primera). La operación a realizar es, por tanto, 1523x3. El resultado (4569) se coloca bajo el último resto y se procede a hallar la diferencia (que es 1467). Una vez realizada la resta se baja el siguiente grupo de cifras y se continúa el proceso. Obsérvese que el número a dividir entre renglón auxiliar y residuo va aumentado.

Paso 7

• Paso 7: Se continúa el mismo proceso, la raíz se vuelve a multiplicar por dos (ignorando el punto de los decimales). El resultado de la multiplicación se agrega al tercer renglón auxiliar, se vuelven a dividir los primeros cuatro números del residuo (1467) entre el resultado de la multiplicación (152), y se obtiene la siguiente cifra para la raíz y el número del renglón auxiliar (9). Dicha cifra se multiplica por el número del tercer renglón auxiliar y se le resta al tercer residuo. Se continua el proceso, si ya no hay más cifras la raíz ha terminado. En este caso, 76.3 se multiplica por 2 como 763 (763x2) que nos da un resultado de 1526. La cifra resultante es 14679 (nótese que son las primeras cuatro cifras, cuando antes eran las tres primeras), y se divide entre 1526, lo que nos da un resultado de 0.9 (como decíamos antes, se toma el primer número aunque sea decimal, por lo tanto, la cifra buscada es 9). El nueve se agrega en el renglón de la raíz y el tercer renglón auxiliar, y se multiplica 9 por 15269, lo que da un resultado de 137421, esta cifra se le resta a 146790 y nos da un resultado de 9369.

La raíz cuadrada de 5836.369 es 76.39, con un residuo de 9369. Recordemos que el cero es sólo un auxiliar. Es importante señalar también que la operación anterior utilizada como ejemplo no está completa. Si la continuáramos daría como resultado 76.396132 (con seis decimales).

Algoritmos para máquinas

Calculadoras, hojas de cálculo y otros softwares también se usan con frecuencia para calcular raices cuadradas. Los programas de software ponen típicamente buenas rutinas en su ejecución para computar la función exponencial y el logaritmo natural o logaritmo, computándose después la raíz cuadrada de x usando la identidad:

${\sqrt {x}}=e^{{\frac {1}{2}}\ln x}$ o ${\sqrt {x}}=10^{{\frac {1}{2}}\log x}$

Se explota la misma identidad al computar raíces cuadradas con tablas de logaritmos o reglas de cálculo...

Extensión de las raíces

La raíz cuadrada en los números complejos

Raíz cuadrada compleja.

Segunda hoja de la raíz cuadrada compleja.

Usando la superficie de Riemann de la raíz cuadrada, uno puede ver cómo las dos hojas caben juntas.

El cuadrado de cualquier número real positivo o negativo es positivo, y el cuadrado de 0 es 0. Por lo tanto, ningún número negativo puede tener una raíz cuadrada en los números reales. Sin embargo, es posible trabajar con un sistema más grande de números, llamados los números complejos, que contienen soluciones a la raíz cuadrada de un número negativo. Esto es hecho introduciendo un nuevo número, denotado por i (a veces j, especialmente en el contexto de la electricidad) y llamado unidad imaginaria, que se define tal que $i^{2}=-1\,\!$. Utilizando esta notación podemos pensar en i como la raíz cuadrada de −1, pero notamos que también tenemos $(-i)^{2}=i^{2}=-1\,\!$, así que (−i) es también una raíz cuadrada de −1. Semejantemente a los números reales, decimos que la raíz cuadrada principal de −1 es i, o, en general, si x es cualquier número real positivo, entonces en la raíz cuadrada principal de −x se cumple la siguiente igualdad:

${\sqrt {-x}}={\sqrt {-1}}{\sqrt {x}}=i{\sqrt {x}}$

es decir, la raíz cuadrada de un número negativo es necesariamente imaginario. Eso es debido a que $i^{2}=-1\,\!$, por lo que entonces:

$\left(i{\sqrt {x}}\right)^{2}=i^{2}{\sqrt {x}}^{2}=(-1)x=-x$

Si se desea encontrar la raíz de un número imaginario es posible demostrar la igualdad

${\sqrt {\pm ix}}={\sqrt {\frac {x}{2}}}\pm i{\sqrt {\frac {x}{2}}}$

Por los argumentos dados, $i$ no puede ser ni positivo ni negativo. Esto crea un problema: para el número complejo $z$, no podemos definir ${\sqrt {z}}$para ser la raíz cuadrada “positiva” de $Z$.

Para cada número complejo diferente a cero z existen exacto dos números W tales que $w^{2}=Z\,\!$. Por ejemplo, las raíces cuadradas de $i$ son:

${\sqrt {i}}={\frac {\sqrt {2}}{2}}(1+i)$

y

$-{\sqrt {i}}=-{\frac {\sqrt {2}}{2}}(1+i).$

La definición general de ${\sqrt {z}}$ está introduciendo el siguiente punto de rama: si z = r e^iφes representado en coordenadas polares con −π < φ ≤ π, después fijamos el valor principal a:

${\sqrt {z}}={\sqrt {r}}\,e^{i\phi \over 2}$

Así definido, la función de la raíz es holomorfa en todas partes excepto en los números reales no positivos, donde no es incluso continua. La antedicha serie de Taylor para ${\sqrt {1+x}}$ sigue siendo válida para el resto de los números complejos x con |x| < 1.

En general, para un número complejo expresado en forma rectangular, se obtiene:

${\sqrt {x+iy}}={\sqrt {\frac {\left|x+iy\right|+x}{2}}}\pm i{\sqrt {\frac {\left|x+iy\right|-x}{2}}}$

donde $\left|x+iy\right|={\sqrt {x^{2}+y^{2}}}$ (el valor absoluto o módulo del número complejo), y el signo de la parte imaginaria de la raíz coincide con el signo de la parte imaginaria del radicando. Observe que debido a la naturaleza discontinua de la función de la raíz cuadrada en el plano complejo, la ley ${\sqrt {zw}}={\sqrt {z}}\cdot {\sqrt {w}}$ es en general falsa. Es incorrecto si se asume que esta ley es la base de varias demostraciones inválidas, por ejemplo el demostrar que $-1=1\,\!$:

$-1=i\cdot i={\sqrt {-1}}\cdot {\sqrt {-1}}={\sqrt {-1\cdot (-1)}}={\sqrt {1}}=1$

donde la tercera igualdad no puede ser justificada.

Este problema puede presentarse como un uso erróneo de la raíz cuadrada principal de notación √ definido en el principio del artículo, o descuidar explicar el punto de rama o descuidando explicar la rama cortada en la definición de la raíz cuadrada compleja de una función. Con el concepto general (dos valores) de la raíz cuadrada, es de hecho verdad que una de las dos raíces cuadradas de 1 es -1.

No obstante, la ley puede ser solamente incorrecta por un factor -1 (es cierto salvo un factor –1), √(zw) = ±√(z)√(w), es cierto o para ± como + o como -. Nótese que √(c²) = ±c, por lo tanto √(a²b²) = ±ab y por lo tanto√(zw) = ±√(z)√(w),usando a = √(z) and b = √(w).

Cada número complejo se puede escribir en su forma polar como $re^{i\theta }$, y ya que

$ae^{i\alpha }\times be^{i\beta }=\left(ab\right)e^{i\left(\alpha +\beta \right)}$

entonces es fácil ver que

${\sqrt {re^{i\theta }}}={\sqrt {r}}~e^{i{\frac {\theta }{2}}}$

Raíz cuadrada de matrices

La existencia de un producto de matrices permite definir la raíz de una matriz como aquella matriz que multiplicada por sí misma da la original.

Si $A$ es una matriz definida positiva u operador, entonces existe exactamente una matriz definida positiva u operador $B$ tal que $B^{2}=A$; entonces definimos ${\sqrt {A}}=B$

Más generalmente, para cada matriz u operador normal $A$ existen operadores normales $B$ tales que $B^{2}=A$. En general, hay muchos de esos operadores $B$ para cada $A$ y entonces la función raíz cuadrada no puede ser definida satisfactoriamente para operadores normales. En cierta manera se puede decir que los operadores definidos positivos son similares a los números reales positivos, y los operadores normales son similares a los números complejos.

Construcción geométrica de la raíz cuadrada

Una raíz cuadrada puede ser construida con regla y compás. En sus Elementos, Euclides (300 AC) dio la construcción de la media geométrica de dos cantidades en sus proposiciones II.14 y VI.13. Dado que la media geométrica de $a$ y $b$ es ${\sqrt {ab}}$, uno puede construir ${\sqrt {a}}$ simplemente tomando $b=1$.

La construcción también fue dada por Descartes en su libro La Géométrie, vea la figura 2 en la segunda página. No obstante, Descartes no afirmo originalidad y su audiencia habría estado bastante familiarizada con Euclides.

Otro método de construcción geométrica usa triángulos rectos e inducción: ${\sqrt {1}}=1$ puede, desde luego, ser construido, y una vez que ${\sqrt {x}}$ ha sido construido, el triángulo recto con 1 y ${\sqrt {x}}$ como catetos, tiene una hipotenusa de ${\sqrt {x+1}}$.

Pasos a seguir para la construcción geométrica

AO = 1, OB = a, OH = x

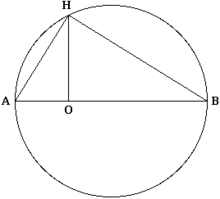
Para calcular la raíz cuadrada de un número mediante una construcción geométrica los pasos a seguir son los siguientes:

1. Trazamos un segmento $a\,\!$ de la longitud del número que queramos calcular su raíz cuadrada.
2. Extendemos ese segmento de medida $a\,\!$ en 1 en la unidad de medida que hayamos tomado el otro, de modo que tengamos el segmento $AB\,\!$ de medida $a+1\,\!$.
3. Trazamos un círculo que tenga como diámetro esta medida de $a+1\,\!$.
4. En el punto $O\,\!$, que es donde empieza la extensión de medida 1 en el segmento, trazamos una línea perpendicular al segmento trazado y la línea obtenida que va del punto $O\,\!$ hasta tocar la circunferencia en el punto $H\,\!$ tiene como medida $OH={\sqrt {a}}$.

Esta construcción tiene su importancia en el estudio de los números constructibles.

Demostración de que OH es igual a la raíz cuadrada de OB

Antes de demostrar la igualdad primero hay que demostrar que los triángulos $AHO\,\!$ y $OHB\,\!$ son triángulos semejantes a partir de un sistema de ecuaciones pero tomando antes ciertas consideraciones:

1. El ángulo $H\,\!$ en su totalidad tiene 90º debido a la propiedad que dice: todo triángulo construido en un círculo ocupando uno de sus lados la diagonal íntegra, cuyos dos vértices sean los lados opuestos de la diagonal tomada y el otro un punto cualquiera de la circunferencia, ha de tener el ángulo que no toca la diagonal en cuestión siempre una abertura de 90º.
2. Ya que en los pasos seguidos pasa su construcción la línea $OH\,\!$ tenía que ser expresamente perpendicular a $AB\,\!$ entonces los dos ángulos formados con $O\,\!$, tanto el derecho como el izquierdo que en conjunto suman a éste, tienen que tener cada uno 90º.
3. La suma de todos los lados de un triángulo da como resultado 180º.

Ahora teniendo en cuenta todo esto construimos el siguiente sistema de ecuaciones:

1. $180=90+B+(90-H_{i})\,\!$
2. $180=90+A+H_{i}\,\!$

Donde $H_{i}\,\!$ es el ángulo superior del triángulo izquierdo del cual desconocemos su abertura, las otras letras representan los otros ángulos que desconocemos y el ángulo $H_{d}\,\!$ se puede representar como la resta de $90-H_{i}\,\!$ ya que 90º es el valor de $H\,\!$ entero. Al resolver la primera ecuación vemos que:

$180=90+B+90-H_{i}\,\!$;

$H_{i}=B\,\!$.

Con lo que ya demostramos que estos ángulos miden lo mismo y al resolver el segundo:

$90=A+H_{i}\,\!$;

$A=90-H_{i}\,\!$.

Con lo que al ser $90-H_{i}=H_{d}\,\!$ se saca que $A=H_{d}\,\!$ y con esto queda demostrado que al medir todos los ángulos lo mismo son triángulos semejantes de manera $AH_{i}O_{i}\,\!$ ~ $H_{d}BO_{d}\,\!$. Al poseer esta semejante los lados de los triángulos tienen una proporcionalidad igual para los tres lados tal que:

${\frac {OH}{1}}={\frac {OB}{OH}}={\frac {HB}{AH}}$

Recordando que al construir geométricamente la raíz $AO\,\!$ siempre valía 1, con lo que cogiendo lo que nos interesa desarrollamos:

${\frac {OH}{1}}={\frac {OB}{OH}}$;

$OB=OH^{2}\,\!$;

$OH={\sqrt {OB}}$.

Quedando demostrada la construcción.

Propiedades

Propiedades generales

Gráfica de la ecuación: $y^{2}=x$

La función raíz cuadrada $f(x)={\sqrt {x}}$ es una función cuyo dominio e imagen es el conjunto $\left[0,\infty \right)$ (el conjunto de todos los números reales no negativos). Esta función regresa un valor que es único. Las siguientes propiedades de la raíz cuadrada son válidas para todos los números reales no negativos x, y:

• ${\sqrt {xy}}={\sqrt {x}}{\sqrt {y}}$
• ${\sqrt {\frac {x}{y}}}={\frac {\sqrt {x}}{\sqrt {y}}}$
• ${\sqrt {x}}=x^{\frac {1}{2}}$
• La función raíz cuadrada, en general, transforma números racionales en números algebraicos; ${\sqrt {x}}$ es racional si y sólo si $x\,$ es un número racional que puede escribirse como fracción de dos cuadrados perfectos. Si el denominador es $1^{2}=1\,$, entonces se trata de un número natural. Sin embargo, ${\sqrt {2}}$ es irracional.
• La interpretación geométrica es que la función raíz cuadrada transforma la superficie de un cuadrado en la longitud de su lado.
• Contrariamente a la creencia popular, ${\sqrt {x^{2}}}$ no necesariamente es igual a $x$. La igualdad se mantiene sólo para los números no negativos $x$, pero cuando $x<0$, ${\sqrt {x^{2}}}$ es un número positivo, y entonces ${\sqrt {x^{2}}}=-x$. Por lo tanto, ${\sqrt {x^{2}}}=\left|x\right|$ para todos los números reales $x$ (véase valor absoluto).
• Suponga que $x$ y $a$ son números reales, y que $x^{2}=a$, y se desea encontrar $x$. Un error muy común es "tomar la raíz cuadrada" y deducir que $x={\sqrt {a}}$. Esto es incorrecto, porque la raíz cuadrada de $x^{2}$ no es $x$, sino el valor absoluto $\left|x\right|$, una de las reglas descritas anteriormente. Luego entonces, todo lo que se puede concluir es que $\left|x\right|={\sqrt {a}}$, o equivalentemente $x=\pm {\sqrt {a}}$.
• En cálculo, cuando se prueba que la función raíz cuadrada es continua o derivable, o cuando se calculan ciertos límites, la siguiente igualdad es muy útil (consiste en multiplicar y dividir por el conjugado, véase Binomio conjugado):

${\sqrt {x}}-{\sqrt {y}}={\frac {x-y}{{\sqrt {x}}+{\sqrt {y}}}}$

y es válida para todos los números no negativos $x$ e $y$ que no sean ambos cero.

• La función ${\sqrt {x}}$ es continua para todos los números no negativos $x,$ y derivable para todos los números positivos $x$ (no es derivable para $x=0$ ya que la pendiente de la tangente ahí es ∞). Su derivada está dada por

$f'(x)={\frac {1}{2{\sqrt {x}}}}$

• Las Series de Taylor de ${\sqrt {x+1}}$ en torno a $x=0$ se pueden encontrar usando el Teorema del binomio:

${\sqrt {x+1}}\,\!$	$=\sum _{n=0}^{\infty }{\frac {(-1)^{n}(2n)!}{(1-2n)n!^{2}4^{n}}}x^{n}$
	$=1+{\frac {1}{2}}x-{\frac {1}{8}}x^{2}+{\frac {1}{16}}x^{3}-{\frac {5}{128}}x^{4}+\dots$
para $\left|x\right|<1$.

Radicales jerarquizados cuadrados

La identidad $2={\sqrt {2+2}}$ implica que $2={\sqrt {2+{\sqrt {2+2}}}}$, y por repeticiones sucesivas:

$2={\sqrt {2+{\sqrt {2+{\sqrt {2+{\sqrt {2+\cdots }}}}}}}}$

Por razones análogas se obtiene:

$3={\sqrt {6+{\sqrt {6+{\sqrt {6+{\sqrt {6+\cdots }}}}}}}}$;

o que

$4={\sqrt {12+{\sqrt {12+{\sqrt {12+{\sqrt {12+\cdots }}}}}}}}$;

...

Si r es una entidad estrictamente superior a uno,

$r={\sqrt {r(r-1)+{\sqrt {r(r-1)+{\sqrt {r(r-1)+{\sqrt {r(r-1)+\cdots }}}}}}}}$

Esta forma de expresar números mediante la repetición sucesiva de números contenidos dentro de raíces cuadradas puede tener diversas aplicaciones como la resolución de algunos tipos de ecuación o la expresión de algunos números famosos como el número áureo o el número pi.

Fracciones continuas

Uno de los resultados más intrigantes del estudio de números irracionales como fracciones continuas fue obtenido por Joseph-Louis Lagrange cerca de 1780. Lagrange descubrió que la raíz cuadrada de cualquier número entero positivo no cuadrado se puede representar por una fracción continua periódica, es decir, donde ocurre cierto patrón de dígitos repetidamente en los denominadores. En un sentido estas raíces cuadradas son números irracionales mucho más simples, porque pueden ser representadas con un patrón de dígitos de repetición simple.

${\sqrt {11}}=3+{\cfrac {1}{3+{\cfrac {1}{6+{\cfrac {1}{3+{\cfrac {1}{6+{\cfrac {1}{\ddots }}}}}}}}}}\,$

Aproximaciones enteras

Los diseñadores de presentaciones de videojuegos tienen a veces necesidad de construir tablas de partes enteras de las raíces cuadradas de los enteros naturales. Las primeras dadas por:

CUADRADO	0	1	2	3	4	5	6	7	8	9	10	...	15	16	17	...	24	25	26	27
RAÍZ	0	1	1	1	2	2	2	2	2	3	3	...	3	4	4	...	4	5	5	5

Una observación de los primeros términos ponen de manifiesto que la construcción para de enteros en enteros, y se salta sucesivamente un incremento de manera regular. Más precisamente:

• El cero es repetido una vez.
• El 1 tres veces.
• El 2 cinco veces
• El 3 siete veces.
• El 4 nueve veces.

El número de veces que el entero n es repetido es el n-ésimo entero impar. La prueba reside sobre la identidad siguiente:

$(a+1)^{2}-a^{2}=2a+1\,$

Raíces cuadradas útiles

Raíz cuadrada de 2.

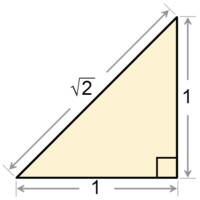
Raíz cuadrada de 2

Quizás la raíz cuadrada más útil es ${\sqrt {2}}$, también conocida como constante pitagórica, que es geométricamente la medida de la hipotenusa de un triángulo rectángulo cuyos dos catetos miden la unidad (ver imagen), pudiéndose demostrar mediante el teorema de Pitágoras:

$1^{2}+1^{2}=x^{2}\,\!$

$x={\sqrt {2}}$

Probablemente la raíz cuadrada de 2 fue el primer número irracional descubierto. El valor de este número con 10 cifras decimales por truncamiento es 1,4142135623

Raíz cuadrada de 3

Mide raíz cuadrada de 3, la diagonal de un cubo cuyas aristas miden 1.

La raíz cuadrada de 3: ${\sqrt {3}}$, también conocida como constante de Theodorus, es geométricamente el valor de la diagonal de un cubo cuyas aristas miden la unidad, pudiéndose demostrar con el teorema de Pitágoras. También es la hipotenusa de un triángulo rectángulo cuyos catetos miden 1 y raíz cuadrada de 2. El valor de este número con 10 cifras decimales por truncamiento es 1,7320508075

Raíz cuadrada de 5

La raíz cuadrada de 5: ${\sqrt {5}}$, aparece en la fórmula del número áureo, y es geométricamente la hipotenusa de un triángulo cuyos catetos miden 1 y 2 respectivamente, comprobándose mediante el teorema de Pitágoras. Su valor con 10 cifras decimales por truncamiento es 2,2360679774

Referencias

• Stewart, James (2006). Cálculo: Conceptos y contextos. México D.F.: Thomson. ISBN 970-686-543-8 e ISBN 978-970-686-543-4. 
• Joseph, George Gheverghese (2000). The crest of the peacock: the non-European roots of mathematics (La cresta del pavo real: Raíces no europeas de las matemáticas). Londres. ISBN 0-691-00659-8 e ISBN 978-0-691-00659-8. 
• Smith, David Eugene (1925). History of Mathematics (vol 2) special topics of elementary Mathematics (Historia de las matemáticas, vol 2, asuntos especiales de las matemáticas elementales). Boston. ISBN 0-486-20430-8 e ISBN 978-0-486-20430-7. 
• Anglin, W.S. (Diciembre de 1994). Mathematics: A Concise History and Philosophy (Matemáticas: Una historia y una filosofía concisas). New York. ISBN 0-387-94280-7 e ISBN 978-0-387-94280-3. 

Véase también

• Cuadrado (aritmética)
• Formas de resolver la raíz cuadrada
• Función exponencial
• Función raíz
• Raíz cuadrada de 2
• Raíz cuadrada de 3
• Raíz cuadrada de 5
• Raíz cúbica
• Raíz de la unidad
• Radical jerarquizado
• Residuo cuadrático
• Racionalización de radicales
• Propiedades de la radicación

Enlaces externos

• Wikimedia Commons alberga una categoría multimedia sobre Raíz cuadrada.
• Wikcionario tiene definiciones y otra información sobre raíz.
• Generador de hojas de ejercicios de raíces cuadradas: [1]
• Programa java para hallar la raíz cuadrada de números enteros con muchísimas cifras decimales: [2]