Paridad (física)

En física, una transformación de la paridad (también llamada inversión de la paridad) es el cambio simultáneo en el signo de toda coordenada espacial:

$P:{\begin{pmatrix}x\\y\\z\end{pmatrix}}\mapsto {\begin{pmatrix}-x\\-y\\-z\end{pmatrix}}$

Una representación de una matriz 3×3 de P podría tener un determinante igual a -1, y por lo tanto no puede reducir su rotación. En un plano bidimensional, la paridad no es la misma como la rotación de 180 grados. Es importante que el determinante de la matriz P sea -1, que no ocurre en una rotación de 180 grados en 2 dimensiones. Aquí un cambio de transformación de la paridad del signo de x o de y, no de ambos.

Relaciones de simple simetría

Bajo rotación, en la geometría clásica los objetos pueden ser clasificados en escalares, vectores u tensores de rango mayor. En la física clásica, configuraciones físicas necesitan ser transformadas bajo representaciones de cada grupo simétrico.

En la teoría cuántica, los estados en un espacio de Hilbert no necesitan transformarse bajo representaciones de grupo de rotaciones, pero solo bajo la representación proyectiva. La palabra proyectiva se refiere al hecho que si uno de los proyectos se desfasan del estado, cuando recordamos que la fase de un estado cuántico no es observable, luego la representación proyectiva se reduce a una representación ordinaria. Todas las representaciones son también representaciones proyectivas, pero la conversión no es cierta, por lo tanto la condición de representaciones proyectivas en un estado cuántico es más débil que la condición de representación de un estado clásico.

Las representaciones proyectivas de cualquier grupo son isomorfas a las representaciones ordinarias de una extensión central de grupo. Por ejemplo, representaciones proyectivas de un grupo rotacional de 3 dimensiones, que es de un grupo especial ortogonal SO(3), son representaciones ordinarias de un grupo especial unitario SU(2). Representaciones proyectivas de un grupo de rotación que no son representaciones llamadas espinoriales y así los estados cuánticos pueden transformarse no sólo en tensores si no también en espinoriales.

Si se añade a esto una clasificación por paridad, esto puede ser extendido, por ejemplo, en las nociones de

• escalares (P = 1) y seudoescalares (P= -1) que son rotacionalmente invariantes.
• vectores (P = -1) y vectores axiales (o seudovectores) (P = 1) que ambas transforman como vectores bajo rotación.

Uno puede definir reflexiones tales como

$V_{x}:{\begin{pmatrix}x\\y\\z\end{pmatrix}}\mapsto {\begin{pmatrix}-x\\y\\z\end{pmatrix}},$

que también tiene determinante negativo. Luego, combinándolos con rotaciones uno puede generar que la transformación de la paridad tenga un determinante positivo, y por lo tanto puede obtener una rotación. Se usa reflexiones para extender la noción de escalares y vectores a seudoescalares y seudovectores.

Las formas de paridad de un grupo abeliano Z₂ debido a una relación P² = 1. Todo grupo abeliano tiene solo una representación irreductible dimensional. Para Z₂, hay dos representaciones irreductibles: uno es par bajo paridad (P φ = φ), la otra es impar (P φ = –φ). Es muy útil en mecánica cuántica. Sin embargo, como se detallará a continuación, bajo representaciones proyectivas y así en principio una transformación de la paridad puede rotar de un estado a otro por cualquier fase.

Se dice que un objeto físico presenta simetría P si es invariante respecto a cualquier operación de simetría como las anteriormente descritas, consistentes en cambiar el signo de una de las coordenadas espaciales.

Física Clásica

Las ecuaciones de Newton del movimiento F = m a (si la masa es constante) iguala dos vectores, y por lo tanto es invariante bajo paridad. La ley de gravitación también envuelve solo vectores y es también, por lo tanto, invariante bajo paridad. Sin embargo el momento angular L es un vector axial.

L = r × p,

P(L) = (-r) × (-p) = L.

En la electrodinámica clásica, la densidad de carga ρ es un escalar, el campo eléctrico E y la corriente j son vectores, pero el campo magnético B es un vector axial. Sin embargo, las ecuaciones de Maxwell son invariantes ante la paridad porque la curva del vector axial es un vector.

Respecto al comportamiento bajo inversión espacial, las variables de la mecánica clásica pueden ser clasificadas en magnitudes pares y magnitudes impares.

Magnitudes pares

Las variables clásicas que no cambian bajo inversión espacial incluyen:

$\ t$, el tiempo cuando ocurre el evento

$\ E$, la energía de la partícula

$\ P$, Potencia (tasa del trabajo realizado)

$\mathbf {L}$, el momento angular de una partícula (ambos, el orbital y el spín)

$\ \rho$, la densidad de carga eléctrica

$\ V$, el potencial eléctrico (voltaje)

$\mathbf {B}$, la inducción magnética

$\mathbf {H}$, el campo magnético

$\mathbf {M}$, la magnetización

$\rho$ la densidad de energía del campo electromagnético

$\ T_{ij}$ tensor de Maxwell

todas las masas, cargas, constantes de acoplamiento y otras constantes físicas excepto las asociadas con la fuerza débil.

Magnitudes impares

Variables clásicas que han invertido su signo por una inversión espacial, incluyen:

$\mathbf {x}$, la posición de una partícula en el espacio tridimensional

$\mathbf {v}$, la velocidad de una partícula

$\mathbf {a}$, la aceleración de una partícula

$\mathbf {p}$, el momento lineal de una partícula

$\mathbf {F}$, la fuerza de una partícula

$\mathbf {J}$, la densidad de corriente eléctrica

$\mathbf {E}$, el campo eléctrico

$\mathbf {D}$, el desplazamiento eléctrico

$\mathbf {P}$, la polarización eléctrica

$\mathbf {A}$, el Potencial vector electromagnético

Mecánica Cuántica

Posibles valores propios

Dos representaciones dimensionales de paridad son dadas por un par de estados cuánticos que van entre ellos sobre la paridad. Sin embargo, ésta representación puede siempre ser reducida a combinaciones lineales de estados, cada uno de ellos es par o impar bajo la paridad. Se dice que todas las representaciones irreductibles de la paridad son de dimensión 1.

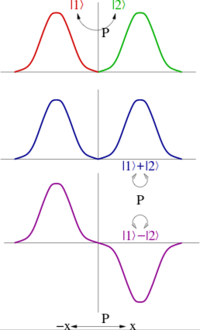
En mecánica cuántica, las transformaciones de espacio-tiempo actúan en estados cuánticos. La transformación de paridad, P es un operador unitario en mecánica cuántica, actuando en un estado ψ así: P ψ(r) = ψ(-r). Se debe tener P² ψ(r) = e^i φ ψ(r), que en todas las fases es inobservable.

El operador P², que invierte la paridad de un estado dos veces, deja la invarianza del espacio-tiempo y así es una simetría interna que rota el estado propio de su fase e^i φ. Si P² es un elemento de e^i Q de un grupo simétrico continuo U(1) de rotaciones en fase entonces e^-i Q/2 es parte de ese U(1) y así es también una simetría. En particular podemos definir P=Pe^-i Q/2 que es también una simetría y así puede llamar a P nuestro operador paridad inscrito como P. Note que P²=1 y así P tiene un valor propio de ±1. Sin embargo cuando no existe tal grupo de simetría, puede ser que todas las transformaciones de la paridad tengan algunos valores propios que son en fase u otros con ±1.

Consecuencias de la paridad simétrica

Cuando la paridad genera el grupo abeliano Z₂, uno puede siempre tomar combinaciones lineales de estados cuánticos tales que sean pares o impares bajo paridad (véase en la figura). Entonces la paridad de tal estado es ±1. La paridad de un estado multiparticular es el producto de las paridades de cada estado; in otras palabras es un número cuántico multiplicativo.

En mecánica cuántica, los hamiltonianos son invariantes (simétricos) bajo transformaciones de paridad si P conmuta con el hamiltoniano. En la mecánica cuántica no relativista, esto ocurre para cualquier potencial que sea escalar, por ejemplo, V = V(r), por lo que el potencial es esférico simétricamente. Los siguientes hechos pueden ser fácilmente probados:

• Si |A> y |B> tienen la misma paridad, entonces <A| X |B> = 0 donde X es el operador posición.
• Para un estado |L, m> de momento angular orbital L con proyección en el eje z m, P |L, m> = (-1)^L|L, m>.
• Si [H, P] = 0, cuando no ocurren transiciones entre estados de paridad opuesta.
• Si [H, P] = 0, entonces un estado propio no-degenerativo de H es también un estado propio de un operador paridad; p.e. una función propia no-degenerativa de H es o bien invariante para P o es cargada en un signo por P'.

Algunas de las funciones propias no-degenerativas de H no se alteran (invariantes) por la paridad P y los otros se limitan a invertir el signo cuando un operador hamiltoniano y un operador de paridad conmutan:

P Ψ = c Ψ,

donde c es una constante, el valor propio de P,

P P Ψ = P c Ψ.

Teoría Cuántica de Campos

La paridad intrínseca asignada en esta sección son verdaderos para la mecánica cuántica relativista como una teoría cuántica de campos.

Si podemos mostrar que el estado de vacío es invariante bajo paridad (P |0> = |0>), el hamiltoniano es invariante de paridad ([H, P] = 0) y las condiciones de cuantización se mantienen sin cambio bajo la paridad, entonces de ello se desprende que cada estado tiene una buena paridad y esa paridad se conserva en cualquier reacción.

Para mostrar que la electrodinámica cuántica es invariante bajo paridad, tenemos que probar que la acción es invariante y la cuantización es también invariante. Por simplicidad asumiremos que la cuantización canónica se utilizada; el estado de vacío es el invariante bajo paridad por ecuaciones. La invarianza de la acción continúa desde la invarianza clásica de Maxwell depende de la transformación del operador aniquilación:

P a(p,±) P⁺  = -a(-p,±)

donde p denota el momento de un fotón y ± se refiere a su estado de polarización. Este es equivalente a la afirmación de que el fotón tiene paridad intrínseca impar. Similarmente todos los bosones vectoriales pueden ser mostrados como paridad intrínseca impar, y todo vector axial tiene paridad par intrínseca.

Hay una sencilla extensión de estos argumentos en teoría de campos escalares que muestra que los escalares tienen paridad par, así:

P a(p) P⁺  = a(-p).

Esto es verdad para campos escalares complejos. (Detalles de espinoriales son mejor detallados en el artículo de la ecuación de Dirac, donde se muestra que los fermiones y antifermiones tienen paridad intrínseca opuesta.). Con los fermiones, hay una complicación simple porque hay mas que un grupo de pin.

Paridad en el modelo estándar

Fijando las simetrías globales

En el modelo estándar de las interacciones fundamentales, hay precisamente tres grupos de simetría global interna U(1) disponible, con cargas igual al número barionico B, el número de leptones L y la carga eléctrica Q. El producto del operador paridad con cualquier combinación de esas rotaciones es otro operador paridad. Es una convención el buscar una combinación específica de esas rotaciones para definir a un operador estándar de paridad y otros operadores de paridad son relacionados al estándar uno por rotaciones internas. Un camino para fijar un operador de paridad estándar es asignando las paridades de tres partículas con con cargas B, L y Q linealmente independientes. En general se asigna la paridad de las más comunes partículas masivas: el protón, el neutrón y el electrón como +1.

Steven Weinberg mostró que si P²=(-1)^F, donde F es el operador del número fermión, entonces si el número fermión es la suma del número leptón mas el número barión, F=B+L, para todas las partículas en el modelo estándar y así el número leptón y el número barión son cargas Q de simetría contínua e^i Q, es posible redefinir el operador paridad de esta manera P²=1. Sin embargo, si hay un neutrino majorana, que los experimentadores creen en su existencia, su número fermión sería igual al de Majorana, y así (-1)^f podría no estar unido con un grupo de simetría contínuo. Los neutrinos de Majorana deberían tener paridad ±i.

Paridad del pión

En un paper de 1954 Absorption of Negative Pions in Deuterium: Parity of the Pion, de William Chinowsky y Jack Steinberger se demostró que el pión π tenía paridad negativa. Ellos estudiaron que el desintegramiento de un átomo hace de un núcleo de deuterio d y un pion π^- cargado negativamente en un estado con momento angular orbital cero L=0 en dos neutrones n

$d\ \pi ^{-}\longrightarrow n\ n.$

Neutrones son fermiones y por lo tanto obedecen a las estadísticas de Fermi, que implican que el estado final es antisimétrico. Usando el hecho de que el deuterón tiene com spín uno y el pión cero, juntos con la antisimetría del estado final, concluyen que los dos neutrones deben tener momento angular orbital L=1. La paridad total es el producto de la paridad intrínseca de partículas y la paridad extrinseca (-1)^L. Así el momento orbital cambia de cero a uno en el proceso, si el proceso es para conservar la paridad total entonces el producto de las paridades intrínsecas de las partículas iniciales y finales debe tener signo opuesto. Un núcleo de deuterio esta hecho de un protón y un neutrón, y usando la antes mencionada convención de que protones y neutrones tienen paridad intrínseca igual a +1 se argumentó que la paridad del pión es igual a menos el producto de las partículas de dos neutrones divididos por el protón y el neutrón en el deuterio, (-1)(1)²/(1)², que es igual a menos 1. Así se concluye que el pión es una partícula seudo escalar.

Violación de la Paridad

La paridad se conserva en electromagnetismo, interacción fuerte y gravitación, y se la viola en la interacción débil. El modelo estándar incorpora la violación de la paridad al expresar a la interacción débil como la interacción quiral de gauge. Solo los componentes zurdos de las partículas y los componentes diestros de las antipartículas participan en la interacción débil en el modelo estándar. Esto implica que la paridad no es simétrica en nuestro universo, a menos que la antimateria exista en esta paridad que se violaría en otro sentido.

La historia de los descubrimientos de la violación de la paridad es interesante. Se sugirió muchas veces y en diferentes contextos que la paridad podría no conservarse, pero en la ausencia de evidencia concreta nunca se los tomo en serio. Una revisión cuidadosa de los físicos teóricos Tsung-Dao Lee y Chen Ning Yang fue más allá, mostrando que mientras la conservación de la paridad ha sido verificada en decaimientos de la fuerza fuerte o de la interacción electromagnética, no fue probada en la interacción débil. Ellos propusieron muchos posibles experimentos directos, los cuales fueron casi en su totalidad ignorados, pero Lee fue capaz de convencer a su colleague de Columbia en probarlos. Ella necesitaba facilidades especiales de criogenia y experiencia, esta fue dada por el Bureau Nacional de Estándares.

En 1956-1957 Wu, E. Ambler, R. W. Hayward, D. D. Hoppes, y R. P. Hudson encontraron una clara violación de la conservación de la paridad en la desintegración beta de Cobalto-60. Como el experimento fue terminado con un doble chequeo en progreso, Wu informó a sus colegas de Columbia sobre sus resultados positivos. Tres de ellos, R. L. Garwin, Leon Lederman, y R. Weinrich modificaron el experimento en el ciclotron e inmediatamente verificaron la violación de la paridad. La publicación se retrasó hasta que el grupo de Wu estuviera listo, los dos papers aparecieron uno detrás del otro.

Después de ese hecho, se notó que un oscuro experimento de 1928 tenía en efecto reportes de la violación de la paridad en desintegraciones débiles pero como el concepto apropiado no había sido inventado aún, no tuvo impacto. El descubrimiento de la violación de la paridad explicó inmediatamente el enigma τ-θ en la física del kaón.

Paridad intrínseca de los hadrones

A cada partícula uno puede asignar una paridad intrínseca cuan grande como su naturaleza preserve la paridad. Por lo tanto la interacción débil no lo hace, se puede aun asignar una paridad a cualquier hadrón al examinar la reacción de una interacción fuerte que la produce o a través de desintegraciones que envuelven a la interacción débil, tal como

π⁰ → γγ.

Véase también

• Simetría C
• Simetría T
• Simetría P
• Simetría CPT
• Modelo estándar
• Física de Partículas
• Teoría electrodébil

Referencias

• CP violation, by I.I. Bigi and A.I. Sanda (ISBN 0-521-44349-0)