Curva cúbica plana

Una selección de curvas cúbicas. Hágase clic en la imagen para ver la página de información con más detalles

En matemáticas, una curva cúbica plana es una curva algebraica bidimensional C definida por una ecuación cúbica​

$F(x,y,z)=0$

aplicada sobre un sistema de coordenadas homogéneas x:y:z para el plano proyectivo; o la versión no homogénea para el espacio afín, determinada mediante el establecimiento de la condición de que z = 1 en dicha ecuación. Aquí F es una combinación lineal distinta de cero de los monomios de tercer grado

x³, y³, z³, x²y, x²z, y²x, y²z, z²x, z²y, xyz.

Se tiene un total de diez monomios; y por lo tanto, las curvas cúbicas forman un espacio proyectivo de dimensión 9 sobre cualquier campo numérico dado K. Cada punto P impone una condición lineal única en F, si se pide que C pase a través de P. Por lo tanto, se puede encontrar alguna curva cúbica a través de un conjunto cualquiera de nueve puntos dados, que pueden ser degenerados y pueden no ser únicos, pero serán únicos y no degenerados si los puntos están en posición general. Esta propiedad se puede comparar con los dos puntos que determinan una recta y con los cinco puntos que determinan una cónica. Si dos cúbicas pasan por un conjunto dado de nueve puntos, entonces, de hecho, un haz de cúbicas también lo hace, y los puntos satisfacen propiedades adicionales; tal como establece el teorema de Cayley-Bacharach.

Cúbica singular y² = x² ⋅ (x + 1). Se puede parametrizar como t ↦ (t² − 1, t ⋅ (t² − 1))

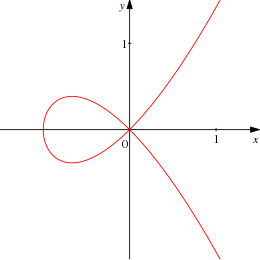
Una curva cúbica puede tener un punto singular, en cuyo caso tiene una parametrización en términos de una recta proyectiva. De lo contrario, se sabe que una curva cúbica no singular tiene nueve puntos de inflexión, sobre un campo cerrado algebraicamente como los números complejos. Esto se puede demostrar tomando la versión homogénea de la matriz hessiana, que define nuevamente una cúbica, y se cruza con C. Las intersecciones se contabilizan mediante el teorema de Bézout. Sin embargo, solo tres de estos puntos pueden ser reales, de modo que los otros no pueden verse en el plano proyectivo real dibujando la curva. Los nueve puntos de inflexión de una cúbica no singular tienen la propiedad de que cada recta que pasa por dos de ellos contiene exactamente tres puntos de inflexión.

Isaac Newton estudió los puntos reales de las curvas cúbicas. Los puntos reales de una cúbica proyectiva no singular se localizan en uno o dos 'óvalos'. Uno de estos óvalos cruza cada recta proyectiva real y, por lo tanto, nunca está delimitado cuando la cúbica se dibuja en el plano euclidiano, y aparece como una o tres ramas infinitas, que contienen los tres puntos de inflexión reales. El otro óvalo, si existe, no contiene ningún punto de inflexión real y aparece como un óvalo o como dos ramas infinitas. Al igual que con las secciones cónicas, una recta corta este óvalo en, como máximo, dos puntos.

Una cúbica plana no singular define una curva elíptica, sobre cualquier campo K para el que tiene un punto definido. Las curvas elípticas ahora se estudian normalmente en alguna variante de las funciones elípticas de Weierstrass, definiendo una extensión cuadrática del campo de funciones racionales realizado mediante la extracción de la raíz cuadrada de una cúbica. Esto depende de tener un K-punto racional, que sirve como el punto del infinito en la forma de Weierstrass. Existen muchas curvas cúbicas que no tienen este punto, por ejemplo, cuando K es el campo de los números racionales.

Los puntos singulares de una curva cúbica plana irreducible son bastante limitados: un punto doble o una cúspide. Una curva cúbica plana reducible es bien una cónica y una recta, o bien tres rectas, y en consecuencia, tiene dos puntos dobles o un tacnodo (si es una cónica y una recta), o hasta tres puntos dobles o un punto triple simple (líneas concurrentes) si se trata de tres rectas.

Curvas cúbicas en el plano triangular

Supóngase que ABC es un triángulo con longitudes de sus lados a = | BC |, b = | CA |, c = | AB |.

En relación con ABC, muchas cúbicas con nombre pasan por puntos conocidos. Los ejemplos que se muestran a continuación utilizan dos tipos de coordenadas homogéneas: trilineales y baricéntricas.

Para convertir de coordenadas trilineales a baricéntricas una ecuación cúbica, se puede utilizar la sustitución siguiente:

x ↦ bcx, y ↦ cay, z ↦ abz;

y para convertir de baricéntricas a trilineales, utilícese

x ↦ ax, y ↦ by, z ↦ cz.

Muchas ecuaciones de curvas cúbicas tienen la forma

f (a, b, c, x, y, z) + f (b, c, a, y, z, x) + f (c, a, b, z, x, y) = 0.

En los ejemplos mostrados a continuación, tales ecuaciones se escriben de manera más sucinta en "notación de suma cíclica". Así:

[suma cíclica f (x, y, z, a, b, c)] = 0.

Las cúbicas listadas a continuación se pueden definir en términos del conjugado isogonal, denotado por X*, de un punto X que no está en una recta lateral de ABC. A continuación se muestra una construcción de X*. Sea L_A el reflejo de la línea XA sobre la bisectriz del ángulo interno del ángulo A; definiéndose L_B y L_C de forma análoga. Entonces las tres líneas reflejadas coinciden en X*. En coordenadas trilineales, si X = x:y:z, entonces X* = 1/x:1/y:1/z.

Cúbica de Neuberg

Ecuación trilineal: [suma cíclica (cos A − 2 cos B cos C)x(y² − z²)] = 0

Ecuación baricéntrica: [suma cíclica (a²(b² + c²) + (b² − c²)² − 2a⁴)x(c²y² − b²z²)] = 0

La cúbica de Neuberg (llamada así por Joseph Jean Baptiste Neuberg) es el lugar geométrico de un punto X, de modo que X* está en la recta EX, donde E es el punto infinito de Euler (X(30) en la Enciclopedia de Centros del Triángulo). Además, esta cúbica es el lugar geométrico de X, de modo que el triángulo X_AX_BX_C es una perspectiva de ABC, donde X_AX_BX_C es el reflejo de X en las líneas BC, CA, AB, respectivamente.

La cúbica de Neuberg pasa por los siguientes puntos: incentro, circuncentro, ortocentro, ambos puntos de Fermat, ambos puntos isodinámicos, el punto de infinito de Euler, otros centros triangulares, los excentros, los reflejos de A, B, C en las líneas laterales de ABC, y los vértices de los seis triángulos equiláteros erigidos sobre los lados de ABC.

Para obtener una representación gráfica y una extensa lista de propiedades de la cúbica de Neuberg, consúltese K001 Cúbicas en el Plano Triangular de Berhard Gibert.

Cúbica de Thomson

Ejemplo de cúbica de Thomson (curva negra). X está en la cúbica, de modo que el conjugado isogonal de X (X') está en la línea X(2)-X

Ecuación trilineal: [suma cíclica bcx(y² − z²)] = 0

Ecuación baricéntrica: [suma cíclica x(c²y² − b²z²)] = 0

La cúbica de Thomson es el lugar geométrico de un punto X tal que X* está en la línea GX, donde G es el centroide.

La cúbica de Thomson pasa por los siguientes puntos: incentro, centroide, circuncentro, ortocentro, punto simétrico, otros centros triangulares, los vértices A, B, C, los excentros, los puntos medios de los lados BC, CA, AB y los puntos medios de las alturas de ABC. Para cada punto P en la cúbica pero no en una línea lateral de la cúbica, el conjugado isogonal de P también está en la cúbica.

Para gráficos y propiedades, véase K002 en Cúbicas en el Plano Triangular.

Cúbica de Darboux

Ecuación trilineal: [suma cíclica (cos A − cos B cos C)x(y² − z²)] = 0

Ecuación baricéntrica: [suma cíclica (2a²(b² + c²) + (b² − c²)² − 3a⁴)x(c²y² − b²z²)] = 0

La cúbica de Darboux es el lugar geométrico de un punto X, de modo que X* está en la línea LX, donde L es el punto de De Longchamps. Además, esta cúbica es el lugar geométrico de X, de modo que el triángulo podal de X es el ceviano de algún punto (que se encuentra en la cúbica de Lucas). Además, esta cúbica es el lugar geométrico de un punto X tal que el triángulo podal de X y el triángulo anticeviano de X se hallan en perspectiva; el centro de la perspectiva se encuentra en la cúbica de Thomson.

La cúbica de Darboux atraviesa el incentro, el circuncentro, el ortocentro, el punto de Longchamps, otros centros triangulares, los vértices A, B, C, los excentros y las antípodas de A, B, C en el circuncírculo. Para cada punto P en la cúbica pero no en una línea lateral de la cúbica, el conjugado isogonal de P también está en la cúbica.

Para gráficos y propiedades, véase K004 en Cúbicas en el Plano Triangular.

Cúbica de Napoleón-Feuerbach

Ecuación trilineal: [suma cíclica cos (B − C)x(y² − z²)] = 0

Ecuación baricéntrica: [suma cíclica (a²(b² + c²) − (b² − c²)²)x(c²y² − b²z²)] = 0

La cúbica de Napoleón-Feuerbach es el lugar geométrico de un punto X* que está en la línea NX, donde N es el centro de nueve puntos (N = X(5) en la Enciclopedia de Centros del Triángulo).

La cúbica de Napoleón-Feuerbach pasa a través del incentro, el circuncentro, el ortocentro, los puntos 1 y 2 de Napoleón, otros centros triangulares, los vértices A, B, C, los excentros, las proyecciones del centroide sobre las alturas y los centros de los 6 triángulos equiláteros erigidos sobre los lados de ABC.

Para gráficos y propiedades, véase K005 en Cúbicas en el Plano Triangular.

Cúbica de Lucas

Ecuación trilineal: [suma cíclica (cos A)x(b²y² − c²z²)] = 0

Ecuación baricéntrica: [suma cíclica (b² + c² − a²)x(y² − z²)] = 0

La cúbica de Lucas es el lugar geométrico de un punto X tal que el triángulo ceviano de X es el triángulo podal de algún punto; el punto está en la cúbica de Darboux.

Las cúbicas de Lucas pasan a través del centroide, ortocentro, punto de Gergonne, punto de Nagel, punto de Longchamps, otros centros de triángulo, los vértices del triángulo anticomplementario, y los focos de la circunelipse de Steiner.

Para gráficos y propiedades, véase K007 en Cúbicas en el Plano Triangular.

Primera cúbica de Brocard

Ecuación trilineal: [suma cíclica bc(a⁴ − b²c²)x(y² + z²)] = 0

Ecuación baricéntrica: [suma cíclica (a⁴ − b²c²)x(c²y² + b²z²)] = 0

Sea A′B′C′ el primer triángulo de Brocard. Para el punto arbitrario X, sean X_A, X_B, X_C las intersecciones de las rectas XA', XB', XC' con las rectas laterales BC, CA, AB, respectivamente. La primera cúbica de Brocard es el lugar geométrico de X para el cual los puntos X_A, X_B, X_C son colineales.

La primera cúbica de Brocard pasa a través del centroide, el punto simmediano, el punto de Steiner, otros centros de triángulos y los vértices de los triángulos 1º y 3º de Brocard.

Para gráficos y propiedades, véase K017 en Cúbicas en el Plano Triangular.

Segunda cúbica de Brocard

Ecuación trilineal: [suma cíclica bc(b² − c²)x(y² + z²)] = 0

Ecuación baricéntrica: [suma cíclica (b² − c²)x(c²y² + b²z²)] = 0

La segunda cúbica de Brocard es el lugar geométrico de un punto X para el cual el polo de la línea XX* en la circuncónica a través de X y X* se encuentra en la línea del circuncentro y el punto simmediano (es decir, el eje de Brocard).

Lal segunda cúbica de Brocard pasa a través del centroide, el punto simmediano, ambos puntos de Fermat, ambos puntos isodinámicos, el punto de Parry, otros centros de triángulos y los vértices de los triángulos 2º y 4º de Brocard.

Para gráficos y propiedades, véase K018 en Cúbicas en el Plano Triangular.

Primera cúbica de áreas iguales

Ecuación trilineal: [suma cíclica a(b² − c²)x(y² − z²)] = 0

Ecuación baricéntrica: [suma cíclica a²(b² − c²)x(c²y² − b²z²)] = 0

La primera cúbica de áreas iguales es el lugar geométrico de un punto X, de modo que el área del triángulo ceviano de X es igual al área del triángulo ceviano de X*. Además, esta cúbica es el lugar geométrico de X para el cual X* está en la recta S*X, donde S es el punto de Steiner. (S = X(99) en la Enciclopedia de Centros del Triángulo).

La primera cúbica de áreas iguales pasa a través del incentro, el punto de Steiner, otros centros triangulares, los puntos de Brocard primero y segundo y los excentros.

Para gráficos y propiedades, véase K021 en Cúbicas en el Plano Triangular.

Segunda cúbica de áreas iguales

Ecuación trilineal: (bz + cx)(cx + ay)(ay + bz) = (bx + cy)(cy + ax)(az + bx)

Ecuación baricéntrica: [suma cíclica a(a² − bc)x(c³y² − b³z²)] = 0

Para cualquier punto X = x:y:z (trilineales), sean X_Y = y:z:x y X_Z = z:x:y. La segunda cúbica de áreas iguales es el lugar geométrico de X, de modo que el área del triángulo ceviano de X_Y es igual al área del triángulo ceviano de X_Z.

La segunda cúbica de áreas iguales pasa a través del incentro, el centroide, el punto simmediano y los puntos indexados en la Enciclopedia de Centros del Triángulo como X(31), X(105), X(238), X(292), X(365), X(672), X(1453), X(1931), X(2053) y otros.

Para gráficos y propiedades, véase K155 en Cúbicas en el Plano Triangular.

Véase también

• Teorema de Cayley-Bacharach, sobre la intersección de dos curvas cúbicas planas
• Cúbica alabeada, una curva cúbica en el espacio
• Curva elíptica
• Bruja de Agnesi

Bibliografía

• Bix, Robert (1998), Conics and Cubics: A Concrete Introduction to Algebraic Curves, New York: Springer, ISBN 0-387-98401-1 . Bix, Robert (1998), Conics and Cubics: A Concrete Introduction to Algebraic Curves, New York: Springer, ISBN 0-387-98401-1 .
• Cerin, Zvonko (1998), «Locus properties of the Neuberg cubic», Journal of Geometry 63 (1–2): 39-56, doi:10.1007/BF01221237 ..
• Cerin, Zvonko (1999), «On the cubic of Napoleon», Journal of Geometry 66 (1–2): 55-71, doi:10.1007/BF01225672 ..
• Cundy, H. M. & Parry, Cyril F. (1995), «Some cubic curves associated with a triangle», Journal of Geometry 53 (1–2): 41-66, doi:10.1007/BF01224039 ..
• Cundy, H. M. & Parry, Cyril F. (1999), «Geometrical properties of some Euler and circular cubics (part 1)», Journal of Geometry 66 (1–2): 72-103, doi:10.1007/BF01225673 ..
• Cundy, H. M. & Parry, Cyril F. (2000), «Geometrical properties of some Euler and circular cubics (part 2)», Journal of Geometry 68 (1–2): 58-75, doi:10.1007/BF01221061 ..
• Ehrmann, Jean-Pierre & Gibert, Bernard (2001), «A Morley configuration», Forum Geometricorum 1: 51-58 ..
• Ehrmann, Jean-Pierre & Gibert, Bernard (2001), «The Simson cubic», Forum Geometricorum 1: 107-114 ..
• Gibert, Bernard (2003), «Orthocorrespondence and orthopivotal cubics», Forum Geometricorum 3: 1-27 ..
• Kimberling, Clark (1998), «Triangle Centers and Central Triangles», Congressus Numerantium 129: 1-295 .. Vea el Capítulo 8 para los cúbicos.
• Kimberling, Clark (2001), «Cubics associated with triangles of equal areas», Forum Geometricorum 1: 161-171 ..
• Lang, Fred (2002), «Geometry and group structures of some cubics», Forum Geometricorum 2: 135-146 ..
• Pinkernell, Guido M. (1996), «Cubic curves in the triangle plane», Journal of Geometry 55 (1–2): 142-161, doi:10.1007/BF01223040 ..
• Salmon, George (1879), Higher Plane Curves (3rd edición), New York: Chelea . Salmon, George (1879), Higher Plane Curves (3rd edición), New York: Chelea ..

Enlaces externos

• Un catálogo de curvas cúbicas planas (versión archivada)
• Puntos en Cúbicas
• Cúbicas en el plano triangular
• Isocúbicas especiales en el triángulo plano (pdf), por Jean-Pierre Ehrmann y Bernard Gibert

• Datos: Q2369721