Función de Gompertz

La curva de Gompertz o la función de Gompertz, es un tipo de modelo matemático para una serie temporal y lleva el nombre de Benjamin Gompertz (1779-1865). Es una función sigmoidea que describe el crecimiento como más lento al comienzo y al final de un período de tiempo dado. La asíntota de la función hacia la derecha o el valor futuro de la función se aproxima de manera mucho más gradual por la curva que la asíntota de la mano izquierda o de valor inferior. Esto contrasta con la función logística simple en la que ambas asíntotas se acercan simétricamente a la curva. Es un caso especial de la función logística generalizada. La función fue diseñada originalmente para describir la mortalidad humana, pero desde entonces se ha modificado para que se aplique en biología, con respecto al detalle de las poblaciones.

Historia

Benjamin Gompertz originalmente diseñó la función para la Royal Society en 1825 para detallar su ley de mortalidad humana. La ley se basa en el supuesto a priori de que la resistencia de una persona a la muerte disminuye a medida que aumentan sus años. El modelo se puede escribir de esta manera:

 $N(T)=a\exp(-b(\exp(-ct)))$

donde:

En este modelo la población parte de cero cuando el tiempo es menos infinito (asíntota horizontal por la izquierda)
$a$ representa la población final de células/organismos (asíntota horizontal por la derecha)
$b$ y $c$ son números positivos que determinan la posición del punto de inflexión de la curva y el valor de la población en el origen, $N(0)$
$c$ denota la tasa de crecimiento poblacional
$\exp$ es la función exponencial.

$N(t)$ representa el número de individuos en el período de tiempo dado, $t$ . Los parámetros $c$ y $a$ son constantes. Este modelo es una modificación de un modelo demográfico de Robert Malthus. Fue comúnmente utilizado por las compañías de seguros para calcular el costo del seguro de vida. Esta ecuación se conoce como una función de Gompertz.

**Gráficos de curvas de Gompertz, que muestran el efecto de variar uno de a, b, c mientras se mantienen constantes los otros**
Variando $a$
Variable $b$
Variable $c$

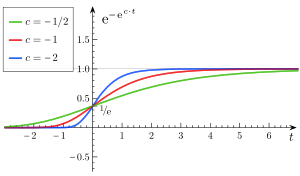Fórmula

 $f(t)=a\mathrm {e} ^{-b\mathrm {e} ^{-ct}},$

donde

a es una asíntota, ya que

 $\lim _{t\to \infty }a\mathrm {e} ^{-b\mathrm {e} ^{-ct}}=a\mathrm {e} ^{0}=a$

b, c es números positivos
b establece el desplazamiento a lo largo del eje x (traduce el gráfico a la izquierda o derecha)
c establece la tasa de crecimiento (escala y)
e es el número de Euler (e = 2.71828...)

Propiedades

El punto medio se encuentra resolviendo

f(t)=a/2

para t.

 $t_{hwp}=-{\frac {\ln(\ln(2)/b)}{c}}$

Cuando $b=ln(2)$ , la función toma el valor $a/2$ en el origen de coordenadas ( $t_{hwp}=0$ ).

El punto de máxima tasa de aumento se encuentra resolviendo ${\frac {d^{2}}{dt^{2}}}f(t)=0$ para t.

 $t_{max}=\ln(b)/c$

Cuando $b=1$ la tasa máxima se alcanza en el origen de coordenadas ( $t_{max}=0$ ).

El aumento en $t_{max}$ es

 $\max \left({\frac {d}{df}}\right)={\frac {ac}{e}}$

Derivación

La curva de función se puede derivar de una ley de mortalidad de Gompertz, que establece que la tasa de mortalidad absoluta (decaimiento) disminuye exponencialmente con el tamaño actual. Matemáticamente,

k^{r}\propto {\frac {1}{y(t)}},

donde

r={\frac {y'(t)}{y(t)}}

es la tasa de crecimiento

k es una constante arbitraria.

Ejemplos de uso

Ejemplos de usos para las curvas de Gompertz incluyen:

La captación de teléfonos móviles, donde los costos fueron inicialmente altos (por lo que la captación fue lenta), seguido por un período de rápido crecimiento, seguida por una disminución de la captación a medida que se alcanzó la saturación.^[1]
Población en un espacio confinado, ya que las tasas de natalidad aumentan primero y luego disminuyen a medida que se alcanzan los límites de recursos.^[2]
Modelización del crecimiento de tumores.
Modelización del impacto del mercado en las finanzas.^[3]
Detallado el crecimiento de la población en animales de presa, con respecto a las relaciones depredador-presa.
Modelización del número de células bacterianas dentro de una población
Propagación de una epidemia

Aplicaciones

Curva de Gompertz

La biología de la población está especialmente preocupada por la función de Gompertz. Esta función es especialmente útil para describir el rápido crecimiento de una cierta población de organismos, al tiempo que también puede explicar la eventual asíntota horizontal, una vez que se determina la capacidad de carga (número de células / población).

Se modela de la siguiente manera:

 $N(t)=N_{0}\exp(\ln(N_{I}/N_{0})(1-\exp(-bt)))$

donde:

$t$ es tiempo
N₀ es la cantidad inicial de células
N_I es el número de población/células de meseta
$b$ es la tasa inicial de crecimiento tumoral

Esta consideración de la función del número de células de meseta lo hace útil para imitar con precisión la dinámica de la población de la vida real. La función también se adhiere a la función sigmoide, que es la convención más aceptada de detallar generalmente el crecimiento de una población. Además, la función hace uso de la tasa de crecimiento inicial, que se observa comúnmente en poblaciones de células bacterianas y cancerosas, que se someten a la fase de registro y crecen rápidamente en número. A pesar de su popularidad, la función de tasa inicial de crecimiento del tumor es difícil de predeterminar, dada la variedad de microcosmos presentes en un paciente, o factores ambientales variables en el caso de la biología de la población. En pacientes con cáncer, factores como la edad, la dieta, el origen étnico, las predisposiciones genéticas, el metabolismo, el estilo de vida y el origen de la metástasis juegan un papel en la determinación de la tasa de crecimiento del tumor. También se espera que la capacidad de carga cambie según estos factores, por lo que es difícil describir tales fenómenos.

Curva metabólica

La función metabólica está particularmente relacionada con la contabilidad de la tasa de metabolismo dentro de un organismo. Esta función se puede aplicar para controlar las células tumorales; la tasa metabólica es dinámica y enormemente flexible, lo que la hace más precisa al detallar el crecimiento del cáncer. La curva metabólica toma en consideración la energía que el cuerpo proporciona para mantener y crear tejido. Esta energía puede considerarse como metabolismo y sigue un patrón específico en la división celular. La conservación de la energía se puede utilizar para modelar dicho crecimiento, independientemente de las diferentes masas y los tiempos de desarrollo. Todos los taxones (un grupo de una o más poblaciones de un organismo) comparten un patrón de crecimiento similar y este modelo, como resultado, considera la división celular, la base del desarrollo de un tumor.

 $B=\sum _{C}(N_{C}B_{C})(E_{C}{\operatorname {d} \!N_{C} \over \operatorname {d} \!t})$

donde:

B = energía que utiliza el organismo en reposo.
N_C = número de células en el organismo dado
B_C = tasa metabólica de una célula individual
N_CB_C = energía requerida para mantener el tejido existente
E_C = energía requerida para crear nuevo tejido a partir de una célula individual

La diferenciación entre la energía utilizada en reposo y el trabajo de la tasa metabólica permite que el modelo determine con mayor precisión la tasa de crecimiento. La energía en reposo es más baja que la energía utilizada para mantener un tejido, y juntas representan la energía requerida para mantener el tejido existente. El uso de estos dos factores, junto con la energía requerida para crear nuevo tejido, traza un mapa completo de la tasa de crecimiento y, además, conduce a una representación precisa de la fase de retraso.

Crecimiento de tumores

En la década de 1960 A.K. Laird^[4] por primera vez utilizó con éxito la curva de Gompertz para ajustar los datos de crecimiento de tumores. De hecho, los tumores son poblaciones celulares que crecen en un espacio confinado donde la disponibilidad de nutrientes es limitada. Al indicar el tamaño del tumor como X (t), es útil escribir la curva de Gompertz de la siguiente manera:

 $X(t)=K\exp \left(\log \left({\frac {X(0)}{K}}\right)\exp \left(-\alpha t\right)\right)=K\left({\frac {X(0)}{K}}\right)^{\exp(-\alpha t)}$

donde:

X (0) es el tamaño del tumor en el momento de la observación de inicio;
K es la capacidad de carga, es decir, el tamaño máximo que se puede alcanzar con los nutrientes disponibles. De hecho es:

 $\lim _{t\rightarrow +\infty }X(t)=K$

independientemente en X(0)>0. Hay que tener en cuenta que, en ausencia de terapias, generalmente es X(0)<K, mientras que, en presencia de terapias, puede ser X (0)>K;

α es una constante relacionada con la capacidad proliferativa de las células
log () se refiere al registro natural.

Es fácil verificar que la dinámica de $X(t)$ se rige por la ecuación diferencial de Gompertz:

 $X^{\prime }(t)=\alpha \log \left({\frac {K}{X(t)}}\right)X(t)$

es decir, es de la forma cuando se desglosa:

X^{\prime }(t)=F\left(X(t)\right)X(t),\quad {\mbox{with}}\quad F^{\prime }(X)\leq 0,

$F(X)$ es la tasa de proliferación instantánea de la población celular, cuya naturaleza decreciente se debe a la competencia por los nutrientes debido al aumento de la población celular, de manera similar a la tasa de crecimiento logístico. Sin embargo, hay una diferencia fundamental: en el caso logístico, la tasa de proliferación para una pequeña población celular es finita:

 $F(X)=\alpha \left(1-\left({\frac {X}{K}}\right)^{\nu }\right)\Rightarrow F(0)=\alpha <+\infty$

mientras que en el caso de Gompertz la tasa de proliferación es ilimitada:

 $\lim _{X\rightarrow 0^{+}}F(X)=\lim _{X\rightarrow 0^{+}}\alpha \log \left({\frac {K}{X}}\right)=+\infty$

Como lo notaron Steel^[5] y Wheldon,^[6] la tasa de proliferación de la población celular está limitada por el tiempo de división celular. Por lo tanto, esto podría ser una evidencia de que la ecuación de Gompertz no es buena para modelar el crecimiento de tumores pequeños. Además, más recientemente, se ha observado^[7] que, incluida la interacción con el sistema inmunológico, Gompertz y otras leyes caracterizadas por F₍₀₎ ilimitado excluirían la posibilidad de vigilancia inmunológica.

Crecimiento de Gompertz y crecimiento logístico.

La ecuación diferencial de Gompertz.

 $X^{\prime }(t)=\alpha \log \left({\frac {K}{X(t)}}\right)X(t)$

es el caso límite de la ecuación diferencial logística generalizada.

 $X^{\prime }(t)=\alpha \nu \left(1-\left({\frac {X(t)}{K}}\right)^{\frac {1}{\nu }}\right)X(t)$

(donde $\nu >0$ es un número entero positivo) ya que

 $\lim _{\nu \rightarrow +\infty }\nu \left(1-x^{1/\nu }\right)=-\log \left(x\right)$ .

Además, hay un punto de inflexión en la gráfica de la función logística generalizada cuando

 $X(t)=\left({\frac {\nu }{\nu +1}}\right)^{\nu }K$

y uno en la gráfica de la función de Gompertz cuando

 $X(t)={\frac {K}{e}}=K\cdot \lim _{\nu \rightarrow +\infty }\left({\frac {\nu }{\nu +1}}\right)^{\nu }$ .

Gomp-ex ley del crecimiento

Basándose en las consideraciones anteriores, Wheldon^[6] propuso un modelo matemático de crecimiento tumoral, denominado modelo Gomp-Ex, que modifica ligeramente la ley de Gompertz..En el modelo Gomp-Ex se supone que inicialmente no hay competencia por los recursos, por lo que la población celular se expande siguiendo la ley exponencial. Sin embargo, hay un umbral de tamaño crítico X_C tal que para X> X_C. La suposición de que no hay competencia por los recursos es cierta en la mayoría de los escenarios. Sin embargo, puede verse afectado por factores limitantes, que requieren la creación de variables de factores secundarios.

el crecimiento sigue la Ley de Gompertz:

 $F(X)=\max \left(a,\alpha \log \left({\frac {K}{X}}\right)\right)$

De modo que:

X_{C}=K\exp \left(-{\frac {a}{\alpha }}\right).

Aquí hay algunas estimaciones numéricas [6] para X_C:^[6] $X_{C}$

$X_{C}\approx 10^{9}$ para tumores humanos
$X_{C}\approx 10^{6}$ para tumores de murinae (ratones)

Véase también

Referencias

↑ Islam, Towhidul; Fiebig, Denzil G.; Meade, Nigel (2002), «Modelling multinational telecommunications demand with limited data», International Journal of Forecasting 18 (4): 605-624, doi:10.1016/S0169-2070(02)00073-0 .
↑ Zwietering, M. H.; Jongenburger, I.; Rombout, F. M.; van 't Riet, K. (1990), «Modeling of the Bacterial Growth Curve», Applied and Environmental Microbiology 56 (6): 1875-1881 .
↑ Caravelli, F.; Sindoni, L.; Caccioli, F.; Ududec, C. (2015), Optimal leverage trajectories in presence of market impact, Bibcode:2016PhRvE..94b2315C, doi:10.1103/PhysRevE.94.022315 .
↑ Laird A. K. (1964). «Dynamics of tumor growth». Br J Cancer 18 (3): 490-502. doi:10.1038/bjc.1964.55.
↑ Steel, G.G. (1977). Growth Kinetics of Tumors. Oxford: Clarendon Press. ISBN 0-19-857388-X.
↑ ^a ^b ^c Wheldon, T.E. (1988). Mathematical Models in Cancer Research. Bristol: Adam Hilger. ISBN 0-85274-291-6.
↑ d'Onofrio A. (2005). «A general framework for modeling tumor-immune system competition and immunotherapy: Mathematical analysis and biomedical inferences». Physica D 208 (3–4): 220-235. Bibcode:2005PhyD..208..220D. doi:10.1016/j.physd.2005.06.032.

Datos: Q1011785

[1] Islam, Towhidul; Fiebig, Denzil G.; Meade, Nigel (2002), «Modelling multinational telecommunications demand with limited data», International Journal of Forecasting 18 (4): 605-624, doi:10.1016/S0169-2070(02)00073-0 .

[2] Zwietering, M. H.; Jongenburger, I.; Rombout, F. M.; van 't Riet, K. (1990), «Modeling of the Bacterial Growth Curve», Applied and Environmental Microbiology 56 (6): 1875-1881 .

[3] Caravelli, F.; Sindoni, L.; Caccioli, F.; Ududec, C. (2015), Optimal leverage trajectories in presence of market impact, Bibcode:2016PhRvE..94b2315C, doi:10.1103/PhysRevE.94.022315 .

[Laird_a-4] Laird A. K. (1964). «Dynamics of tumor growth». Br J Cancer 18 (3): 490-502. doi:10.1038/bjc.1964.55.

[Steel-5] Steel, G.G. (1977). Growth Kinetics of Tumors. Oxford: Clarendon Press. ISBN 0-19-857388-X.

[Wheldon-6] Wheldon, T.E. (1988). Mathematical Models in Cancer Research. Bristol: Adam Hilger. ISBN 0-85274-291-6.

[DOnofrio-7] 'Onofrio A. (2005). «A general framework for modeling tumor-immune system competition and immunotherapy: Mathematical analysis and biomedical inferences». Physica D 208 (3–4): 220-235. Bibcode:2005PhyD..208..220D. doi:10.1016/j.physd.2005.06.032.

[1]

[2]

[3]

[4]

[5]

[6]

[7]