Grupo triangular

Triángulo esférico

Triángulo hiperbólico

En matemáticas, un grupo triangular es un tipo de grupo que se puede caracterizar geométricamente mediante secuencias de reflexiones respecto a los lados de un triángulo. El triángulo puede ser un triángulo euclídeo ordinario, un triángulo esférico o un triángulo hiperbólico. Cada grupo de triángulos es el grupo de simetría de un teselado del espacio bidimensional, de una esfera, o del plano hiperbólico por congruencia de los llamados triángulos de Möbius, cada uno un dominio fundamental para la operación.

Definición

Sean l, m, y n números enteros mayores o iguales a 2. Un grupo triangular Δ(l, m, n) es un grupo de los movimientos del plano euclídeo, la esfera bidimensional, el plano proyectivo real o el plano hiperbólico, generados por las reflexiones respecto a los lados de un triángulo con ángulos π /l, π /m y π /n (medidos en radianes). El producto de las reflexiones en dos lados adyacentes es una rotación según un ángulo que es el doble del ángulo entre esos dos lados, 2π/l, 2π/m y 2π /n. Por lo tanto, si las reflexiones generadoras están etiquetadas como a, b, c y los ángulos entre ellos en el orden cíclico son los indicados anteriormente, entonces se mantienen las siguientes relaciones:

1. $a^{2}=b^{2}=c^{2}=1$
2. $(ab)^{l}=(bc)^{n}=(ca)^{m}=1.$

Es un teorema que todas las demás relaciones entre a, b, c son consecuencias de estas relaciones y que Δ (l, m, n) es un grupo discreto de movimientos del espacio correspondiente. Por lo tanto, un grupo de triángulos es un grupo de reflexión que admite una presentación de grupo

$\Delta (l,m,n)=\langle a,b,c\mid a^{2}=b^{2}=c^{2}=(ab)^{l}=(bc)^{n}=(ca)^{m}=1\rangle .$

Un grupo abstracto con esta presentación es un grupo de Coxeter con tres generadores.

Clasificación

Dado cualquier número natural l, m, n > 1, exactamente una de las geometrías bidimensionales clásicas (euclidiana, esférica o hiperbólica) admite una triángulo con los ángulos (π/l, π/m, π/n), y el espacio está embaldosado por reflejos del triángulo. La suma de los ángulos del triángulo determina el tipo de geometría del teorema de Gauss-Bonnet: es euclidiana si la suma de los ángulos es exactamente π, esférica si excede de π; e hiperbólica si es estrictamente menor que π. Además, cualquiera de los dos triángulos con los ángulos dados son congruentes. Cada grupo de triángulos determina un mosaico, que se colorea convencionalmente en dos colores, de modo que cualquiera de los dos mosaicos adyacentes tenga colores opuestos.

En cuanto a los números l, m, n > 1, existen las siguientes posibilidades.

El caso euclídeo

${\frac {1}{l}}+{\frac {1}{m}}+{\frac {1}{n}}=1.$

El grupo triangular es el grupo de simetría infinito de una determinada teselación (o mosaico) del plano euclídeo mediante triángulos cuyos ángulos suman π (o 180°). Sin considerar permutaciones, el triplete (l, m, n) es uno de los tripletes (2,3,6), (2,4,4), (3,3,3). Los grupos de triángulos correspondientes son elementos de los grupos del papel pintado.

(2,3,6)	(2,4,4)	(3,3,3)
Teselado hexagonal bisecado	Teselado tetraquis cuadrado	Teselado triangular
Diagramas más detallados, etiquetando los vértices y mostrando cómo funciona la reflexión:

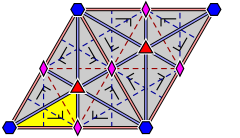
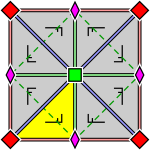
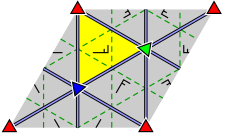
El caso esférico

${\frac {1}{l}}+{\frac {1}{m}}+{\frac {1}{n}}>1.$

El grupo de triángulos es el grupo de simetría finita de un teselado de una esfera unitaria mediante triángulos esféricos, o triángulos de Möbius, cuyos ángulos suman un número mayor que π. Sin considerar permutaciones, el triplete (l, m, n) tiene la forma (2,3,3), (2,3,4), (2,3,5 ), o (2,2, n), n > 1. Los grupos de triángulos esféricos se pueden identificar con los grupos de simetría de los poliedros regulares en el espacio euclidiano tridimensional: Δ(2,3,3) corresponde a un tetraedro; Δ (2,3,4) tanto a un cubo como a un octaedro (que tienen el mismo grupo de simetría); (2,3,5) tanto a un dodecaedro como a un icosaedro. Los grupos Δ(2,2,n), n > 1 del grupo diedral se pueden interpretar como los grupos de simetría de la familia de diedros, que son los sólidos degenerados formados por dos n-ágonos regulares idénticos unidos entre sí, o sus hosoedros duales, que se forman al unir n digonos junto a dos vértices.

El teselado esférico correspondiente a un poliedro regular se obtiene formando la subdivisión baricéntrica del poliedro y proyectando los puntos y líneas resultantes sobre la esfera circunscrita. En el caso del tetraedro, hay cuatro caras ,y cada cara es un triángulo equilátero que se subdivide en 6 trozos más pequeños por las medianas que se intersecan en el centro. La teselación resultante tiene 4 × 6 = 24 triángulos esféricos (es el tetraquishexaedro esférico).

Estos grupos son finitos, lo que corresponde a la compacidad de la esfera: las áreas de los discos en la esfera crecen inicialmente en términos de radio, pero finalmente cubren toda la esfera.

Los teselados triangulares se representan a continuación:

(2,2,2)	(2,2,3)	(2,2,4)	(2,2,5)	(2,2,6)	(2,2,n)
(2,3,3)		(2,3,4)		(2,3,5)

Las teselas esféricas correspondientes al octaedro y al icosaedro y a los teselados esféricos diédricos con n par presentan simetría central. Por lo tanto, cada uno de ellos determina un mosaico del plano proyectivo real, un teselado elíptico. Su grupo de simetría es el cociente del grupo de triángulos esféricos respecto a la simetría central (-I), que es un elemento central de orden 2. Dado que el plano proyectivo es un modelo de geometría elíptica, estos grupos se denominan grupos triangulares elípticos.​

El caso hiperbólico

${\frac {1}{l}}+{\frac {1}{m}}+{\frac {1}{n}}<1.$

El grupo de triángulos es el grupo de simetría infinita de un teselado del plano hiperbólico por triángulos hiperbólicos cuyos ángulos suman un número menor que π. Todos los tripletes que no figuran en la lista representan teselados del plano hiperbólico. Por ejemplo, el triple (2,3,7) produce el grupo triangular (2,3,7). Hay infinitos grupos de este tipo. Los teselados asociados con algunos valores pequeños son:

Plano hiperbólico

Disco de Poincaré de triángulos del dominio fundamental

Ejemplo con triángulos rectángulos (2 p q)
(2 3 7)	(2 3 8)	(2 3 9)	(2 3 ∞)
(2 4 5)	(2 4 6)	(2 4 7)	(2 4 8)	(2 4 ∞)
(2 5 5)	(2 5 6)	(2 5 7)	(2 6 6)	(2 ∞ ∞)
Ejemplo con triángulos generales (p q r)
(3 3 4)	(3 3 5)	(3 3 6)	(3 3 7)	(3 3 ∞)
(3 4 4)	(3 6 6)	(3 ∞ ∞)	(6 6 6)	(∞ ∞ ∞)

Los grupos de triángulos hiperbólicos son ejemplos de un grupo cristalográfico no euclideo, y se han generalizado en la teoría de Gromov sobre grupos hiperbólicos.

Grupos de Von Dyck

Denotar por D (l, m, n) el subgrupo de índice 2 en Δ (l, m, n) creado mediante términos de valor par en los generadores. Dichos subgrupos a veces se denominan grupos de triángulos "ordinarios"​ o grupos de von Dyck, en referencia a Walther von Dyck. Para los triángulos esféricos, euclidianos e hiperbólicos, estos corresponden a los elementos del grupo que conservan la orientación del triángulo (el grupo de las rotaciones). Para los triángulos proyectivos (elípticos), no pueden interpretarse así, ya que el plano proyectivo no es orientable, por lo que no existe la noción de "preservación de la orientación". Sin embargo, las reflexiones son reversiones de orientación "localmente" (y cada variedad es orientable localmente, porque es localmente euclídea): fijan una recta, y en cada uno de sus puntos existe una reflexión respecto a ella.​

El grupo D(l, m, n) se define por la siguiente presentación:

$D(l,m,n)=\langle x,y\mid x^{l},y^{m},(xy)^{n}\rangle .$

En términos de los generadores anteriores, estos son x = ab, y = ca, yx = cb. Geométricamente, los tres elementos x, y, xy corresponden a rotaciones por 2π/l, 2π/m y 2π/n sobre los tres vértices del triángulo.

Téngase en cuenta que D(l,m,n)≅D(m,l,n)≅D(n,m,l), así que D(l,m,n) es independiente del orden de l,m,n.

Un grupo hiperbólico de von Dyck es un grupo fuchsiano, un grupo discreto que consiste en isometrías que conservan la orientación del plano hiperbólico.

Teselados solapados

Véase también: Triángulo de Schwarz

Los grupos triangulares conservan la teselación por triángulos, es decir, un dominio fundamental para la operación (el triángulo definido por las líneas de reflexión), llamado triángulo de Möbius, y están dados por un triplete de "enteros", (l,m,n), - los números enteros corresponden a triángulos (2l,2m,2n) que se unen en un vértice. También existen teselaciones con triángulos solapados, que corresponden a triángulos de Schwarz con números racionales (l/a,m/b,n/c), donde los denominadores son coprimos con respecto a los numeradores. Esto corresponde a los lados que se encuentran en los ángulos de aπ/l (resp.), que corresponde a una rotación de 2aπ/l (resp.), que tiene el orden l y, por lo tanto, es idéntico a un elemento de un grupo abstracto, pero distinto cuando está representado por una reflexión.

Por ejemplo, el triángulo de Schwarz (2 3 3) produce un mosaico de densidad 1 sobre la esfera, mientras que el triángulo (2 3/2 3) produce un mosaico de la densidad 3 sobre la esfera, pero con el mismo grupo abstracto. Estas simetrías de teselaciones solapadas no se consideran grupos triángulares.

Historia

Los grupos triangulares datan, al menos, de la presentación del grupo icosaedral como el grupo de triangular (rotacional) (2,3,5) por William Rowan Hamilton en 1856, en su artículo sobre cálculo icosiano.​

Aplicaciones

Video externo
Teselado modular deformado​ – visualización de la aplicación (2,3,∞) → (2,3,7) por metamorfosis de las teselas asociadas.
Atención: este archivo está alojado en un sitio externo, fuera del control de la Fundación Wikimedia.

Los grupos triangulares aparecen en la geometría aritmética. El grupo modular es generado por dos elementos, S y T, sujeto a las relaciones S² = (ST)³ = 1 (sin relación en T), es el grupo triangular rotacional (2,3, ∞) y se asigna a todos los grupos triangulares (2,3, n) agregando la relación Tⁿ = 1. Más generalmente, el grupo de Hecke H_q está generado por dos elementos, S y T, sujeto a las relaciones S² = (ST)^q = 1 (sin relación en T), es el grupo triangular rotacional (2, q, ∞) y se asigna a todos los grupos de triángulos (2, q, n) al agregar la relación Tⁿ = 1 el grupo modular es el grupo de Hecke H₃. En la teoría de Grothendieck de dessins d'enfants, una función de Belyi da lugar a una teselación de una superficie de Riemann mediante dominios de reflexión de un grupo triangular.

Los 26 grupos esporádicos son cocientes de grupos triangulares,​ de los cuales 12 son grupos de Hurwitz (cocientes del grupo (2,3,7)).

Véase también

• Triángulo de Schwarz
• Función hipergeométrica, una aplicación de triángulos sobre el semiplano superior.
• Teoría geométrica de grupos

Bibliografía

• Magnus, Wilhelm (1974), «II. Discontinuous groups and triangle tessellations», Noneuclidean tesselations and their groups, Academic Press, pp. 52–106, ISBN 978-0-12-465450-1 .
• Gross, Jonathan L.; Tucker, Thomas W. (2001), «6.2.8 Triangle Groups», Topological graph theory, Courier Dover Publications, pp. 279–281, ISBN 978-0-486-41741-7 .
• Wilson, R. A. (2001), «The Monster is a Hurwitz group», Journal of Group Theory 4 (4): 367-374, MR 1859175, doi:10.1515/jgth.2001.027, archivado desde el original el 5 de marzo de 2012, consultado el 10 de septiembre de 2019 .

Enlaces externos

• Robert Dawson Algunos teselados esféricos (sin fecha, anterior a 2004) (Muestra varias teselaciones esféricas interesantes, la mayoría de las cuales no son teselaciones de grupos triangulares)
• Elizabeth r chen triangle groups (2010) Imágenes de fondo de escritorio
• Este artículo incorpora material de Triangle groups en PlanetMath, que tiene licencia Creative Commons Atribución Compartir-Igual.

• Datos: Q652123