Peine del topólogo

El peine del topólogo, en topología, es un conjunto contenido en $\mathbb {R} ^{2}$ utilizado frecuentemente para ilustrar determinadas propiedades de los espacios topológicos. Se utiliza especialmente a modo de ejemplo de espacio topológico que es conexo pero no localmente conexo por caminos o arco-conexo.

Definición

Peine del topólogo

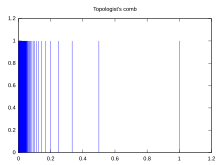
Consideremos $\mathbb {R} ^{2}$ con su topología estándar, y sea $K$ el conjunto $K=\{1/n~|~n\in \mathbb {N} \}$.

El peine del topólogo, $P$, es el subconjunto de $\mathbb {R} ^{2}$ definido por

$P=(\{0\}\times [0,1])\cup (K\times [0,1])\cup ([0,1]\times \{0\})$

El peine reducido, $R$, se define como:

$R=(\{0\}\times \{0,1\})\cup (K\times [0,1])\cup ([0,1]\times \{0\})$.

Es decir, el peine reducido consiste en remover el segmento $\{0\}\times (0,1)$ del peine del topólogo.

Propiedades topológicas

El espacio peine y el espacio peine reducido tienen algunas propiedades topológicas interesantes, sobre todo relacionadas con la noción de conexidad.

1. El espacio peine es un ejemplo de un espacio conexo que no es localmente arco-conexo.

2. El peine reducido es conexo, pero no arco-conexo, ya que no hay ningún camino desde el (0,1) hacia el (0,0).

Véase también

• Seno del topólogo

• Datos: Q5150587