Teorema de Maxwell-Betti

El teorema de Maxwell-Betti, o de forma más completa, teorema de reciprocidad de Maxwell-Betti de resistencia de materiales se debe al matemático italiano Enrico Betti, quien en 1872 generalizó un teorema de Maxwell, publicado a su vez en 1864. Este teorema pertenece a una serie de teoremas energéticos, entre los que se encuentran también los teoremas de Castigliano. La importancia de los teoremas energéticos radica en su potencia en el análisis de estructuras, que se debe a su sencillez y generalidad. Este teorema es también de importancia en el planteamiento del Método de elementos de frontera.

Coeficientes de influencia

Sea un sólido elástico que se somete a un sistema de fuerzas, asumiendo las siguientes hipótesis:

• En cualquier punto del sólido, cada fuerza produce una deformación proporcional a la misma (ley de Hooke: linealidad entre tensiones y deformaciones).
• Se verifica el Principio de superposición.
• La aplicación de cualquier fuerza sobre el sólido no modifica la línea de acción de las restantes cargas aplicadas.
• Las fuerzas se aplican de manera progresiva y lineal, no dando lugar a vibraciones ni a intercambio de calor con el exterior.

Sean i y j dos puntos del sólido elástico, denominándose $\Delta _{ij}\,$ al desplazamiento del punto i al aplicar en j una fuerza $F_{j}\,$. En virtud de la primera de las hipótesis anteriormente citadas, se puede afirmar que:

$\Delta _{ij}\propto F_{j}\,$

Si aplicamos un conjunto de n fuerzas sobre el sólido elástico, aplicando el principio de superposición se tendrá que el desplazamiento total del punto i será:

$\Delta _{i}=\Delta _{i1}+\Delta _{i2}+\cdots +\Delta _{in}\,$

Sea $\delta _{ij}\,$ la proyección del desplazamiento del punto i sobre la dirección de la fuerza aplicada en él, $F_{i}\,$, cuando se aplica en j una carga unitaria $F_{j}^{*}\,$. Estos desplazamientos proyectados sobre la línea de acción de la fuerza son los que producen trabajo (recuérdese que el trabajo se calcula como el producto escalar de la fuerza por el desplazamiento). Definiendo de este modo $\delta _{ij}\,$, y teniendo en cuenta la proporcionalidad entre fuerzas actuantes y deformaciones enunciada anteriormente, se puede expresar el desplazamiento total del punto i proyectado en la dirección de $F_{i}\,$, de la siguiente manera:

$\Delta _{i}=\delta _{i1}F_{1}+\delta _{i2}F_{2}+\cdots +\delta _{in}F_{n}=\sum _{j}{\delta _{ij}F_{j}}$

A los coeficientes $\delta _{ij}\,$ se les denomina coeficientes de influencia y representan la componente del desplazamiento que provoca una carga unitaria aplicada sobre j en el punto i, en la dirección de $F_{i}\,$.

La definición de los coeficientes de influencia se debe a Clapeyron.

Energía de deformación

Supongamos un sólido elástico inicialmente descargado, y que empezamos a cargarlo con una fuerza $\alpha F_{1},\alpha \in (0,1)$. Debido a las hipótesis expresadas anteriormente, existe proporcionalidad entre fuerzas y desplazamientos de modo que a un determinado incremento relativo de la fuerza le corresponde el mismo incremento relativo del desplazamiento, o lo que es lo mismo, la pendiente de una gráfica fuerza-desplazamiento es constante. Y por tanto, a la aplicación de una fuerza $\alpha F_{1}\,$ le corresponderá un desplazamiento $\alpha \delta _{1}\,$.

La energía de deformación acumulada durante todo el proceso de carga será igual al área que queda por debajo de la recta representada en la gráfica fuerza-desplazamiento, es decir, el área de un triángulo:

$W(F_{1})={\frac {1}{2}}F_{1}\delta _{1}\,$

Si el sólido elástico no se carga con una única fuerza, sino con un conjunto de ellas, aplicando el principio de superposición se tiene:

$W(F_{1},F_{2},...)={\frac {1}{2}}\sum _{i}F_{i}{\delta _{i}}$

Teniendo en cuenta lo dicho en el apartado dedicado a los coeficientes de influencia:

$W(F_{1},F_{2},...)={\frac {1}{2}}\sum _{i}F_{i}\sum _{j}\delta _{ij}F_{j}\,$

Teorema de Maxwell-Betti

Enunciado

Sea un cuerpo elástico lineal $\scriptstyle K\in \mathbb {R} ^{3}$ sobre el que actúan dos conjuntos de fuerzas $P_{i}\,$ y $Q_{j}\,$ aplicados sobre los puntos del sólido $A_{i}\,$ y $B_{j}\,$, respectivamente. Sean:

• $\lambda _{i}\,$ los desplazamientos de los puntos $A_{i}\,$
• $\mu '_{j}\,$ los desplazamientos de los puntos $B_{j}\,$ cuando solo actúan sobre el sólido elástico las fuerzas $P_{i}\,$.

Análogamente,

• $\mu _{j}\,$ son los desplazamientos de los puntos $B_{j}\,$
• $\lambda '_{i}\,$ a los desplazamientos de los puntos $A_{i}\,$ cuando solo actúa el conjunto de fuerzas $Q_{j}\,$.

El trabajo realizado por las cargas no depende del orden de aplicación de las mismas, por lo que basta considerar dos casos:

1. Aplicamos en primer lugar el conjunto de fuerzas $P_{i}\,$, resultando la siguiente energía de deformación:

$W(P_{i})={\frac {1}{2}}\sum _{i}P_{i}{\lambda _{i}}$

A continuación añadimos el conjunto $Q_{j}\,$, quedando el total de la energía de deformación como sigue:

$W(P_{i},Q_{j})={\frac {1}{2}}\sum _{i}P_{i}{\lambda _{i}}+{\frac {1}{2}}\sum _{j}Q_{j}{\mu _{j}}+\sum _{i}P_{i}{\lambda '_{i}}$

El segundo término de la ecuación es debido al trabajo realizado por las fuerzas $Q_{j}\,$ sobre sus puntos de aplicación, es decir, $B_{j}\,$, mientras que el tercer término se debe a que durante la aplicación de las fuerzas $Q_{j}\,$ los puntos de aplicación de las fuerzas $P_{i}\,$ se han desplazado una cantidad $\lambda '_{i}\,$, y en consecuencia las fuerzas $P_{i}\,$ habrán realizado un trabajo. Este término no se divide por dos porque es un trabajo realizado por las fuerzas $P_{i}\,$ que han permanecido constantes durante la realización del mismo, a diferencia de los otros dos términos en los cuales el trabajo ha sido realizado durante un proceso de carga del sólido elástico, siendo de aplicación la fórmula deducida en el apartado dedicado a Energía de deformación.

2. En este segundo caso, aplicamos en primer lugar el conjunto de fuerzas $Q_{j}\,$, y a continuación añadimos el conjunto $P_{i}\,$, quedando entonces la energía de deformación como sigue:

$W(Q_{j},P_{i})={\frac {1}{2}}\sum _{j}Q_{j}{\mu _{j}}+{\frac {1}{2}}\sum _{i}P_{i}{\lambda _{i}}+\sum _{j}Q_{j}{\mu '_{j}}$

Del mismo modo que en el primer caso, el tercer término se debe a que durante la aplicación de las fuerzas $P_{i}\,$ los puntos de aplicación de las fuerzas $Q_{j}\,$ se han desplazado una cantidad $\mu '_{j}\,$, y en consecuencia las fuerzas $Q_{j}\,$ realizan un trabajo.

Tal y como se ha dicho al principio, la energía de deformación no depende del orden de aplicación de las cargas por lo que igualando las expresiones obtenidas en los dos casos considerados:

$\sum _{i}P_{i}{\lambda '_{i}}=\sum _{j}Q_{j}{\mu '_{j}}\,$

Esta igualdad es la que da lugar al Teorema de Maxwell-Betti, que puede enunciarse de la siguiente forma:

En un sólido elástico y lineal, siendo $P_{i}\,$ y $Q_{j}\,$ dos sistemas de cargas independientes, se establece que el "trabajo interno" realizado por el sistema de cargas $P_{i}\,$ sobre el campo de desplazamientos producido por el sistema $Q_{j}\,$ es igual al "trabajo interno" realizado por el sistema $Q_{j}\,$ sobre los desplazamientos producidos por el sistema $P_{i}.\,$ Enrico Betti

La principal consecuencia de este resultado es que los coeficientes de influencia recíprocos son iguales. En efecto, supongamos que tanto $P_{i}=Q_{j}=1\,$. Entonces el significado de $\lambda '_{i}\,$ coincide con la definición del coeficiente de influencia $\delta _{ij}\,$, mientras que $\mu '_{j}\,$ se corresponde con el coeficiente de influencia recíproco al anterior, es decir, $\delta _{ji}\,$, y por la expresión que define el Teorema de Maxwell-Betti, se tiene que:

$\delta _{ij}=\delta _{ji}\,$

Este teorema es de aplicación también en el caso de que no sean fuerzas sino momentos (o incluso fuerzas y momentos) las acciones aplicadas sobre el sólido elástico, en cuyo caso los desplazamientos serán sustituidos por el ángulo de rotación correspondiente.

Demostración

Sistemas de fuerzas y desplazamientos

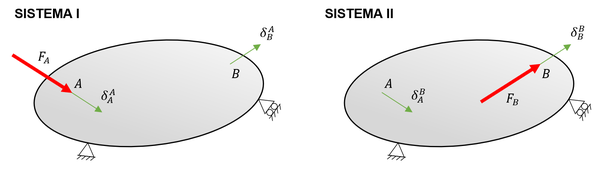
Sea un cuerpo deformable $K\in \mathbb {R} ^{3}$ cuyo comportamiento es elástico-lineal. Sobre él actúan dos fuerzas: $F_{A}$ sobre un punto $A$ cualquiera y $F_{B}$ sobre un punto $B$, cada una de las cuales genera un campo de desplazamientos que, por la linealidad del problema, son mutuamente independientes. Considérese pues que el efecto conjunto sobre el cuerpo deformable es suma de dos sistemas:

• Sistema I. Se aplica la fuerza $F_{A}$, lo cual genera un desplazamiento $\delta _{A}^{A}$ en $A$ y un desplazamiento $\delta _{B}^{A}$ en $B$.
• Sistema II. Se aplica la fuerza $F_{B}$, lo cual genera un desplazamiento $\delta _{B}^{B}$ en $B$ y un desplazamiento $\delta _{A}^{B}$ en $A$.

Nótese que de los desplazamientos en un punto se considera únicamente su valor en la dirección de la carga que se aplica en tal punto. Igualmente, se señala que la notación $\delta _{i}^{j}$ corresponde a un desplazamiento en el punto $i$ debido a la carga aplicada en el punto $j$.

Debido a la linealidad del problema, es aplicable el principio de superposición. Por tanto, el trabajo total realizado aplicando primero el sistema I y luego el sistema II (caso 1) debe ser el mismo que si se aplican al revés (caso 2).

Caso 1. Se aplica primero el sistema I y luego el sistema II

Cuando se aplica el sistema I, la fuerza $F_{A}$ realiza un trabajo al desplazarse $\delta _{A}^{A}$, que, teniendo en cuenta que hay proporcionalidad entre desplazamientos y fuerzas, es el siguiente:

${\dfrac {1}{2}}F_{A}\delta _{A}^{A}$

Al aplicarse el sistema II, la fuerza $F_{B}$ realiza un trabajo al desplazarse $\delta _{B}^{B}$, pero también realiza otro al desplazar $F_{A}$ una cantidad $\delta _{A}^{B}$. En esta última se debe considerar, además, que $F_{A}$ actúa en todo momento con su valor máximo, por lo que no se incorpora el coeficiente de $1/2$. Con esto, el trabajo generado al aplicar el sistema II es:

${\dfrac {1}{2}}F_{B}\delta _{B}^{B}+F_{B}\delta _{A}^{B}$

Con lo que el trabajo total es la suma de ambos y vale:

${\dfrac {1}{2}}F_{A}\delta _{A}^{A}+{\dfrac {1}{2}}F_{B}\delta _{B}^{B}+F_{B}\delta _{A}^{B}$

Caso 2. Se aplica primero el sistema II y luego el sistema I

Cuando se aplica el sistema II, la fuerza $F_{B}$ realiza un trabajo al desplazarse $\delta _{B}^{B}$, que es el siguiente:

${\dfrac {1}{2}}F_{B}\delta _{B}^{B}$

Al aplicarse el sistema I, la fuerza $F_{A}$ realiza un trabajo al desplazarse $\delta _{A}^{A}$, pero también realiza otro al desplazar $F_{B}$ una cantidad $\delta _{B}^{A}$. Con esto, el trabajo generado al aplicar el sistema I es:

${\dfrac {1}{2}}F_{A}\delta _{A}^{A}+F_{A}\delta _{B}^{A}$

Sumando lo previo, el trabajo total en este nuevo caso vale:

${\dfrac {1}{2}}F_{A}\delta _{A}^{A}+{\dfrac {1}{2}}F_{B}\delta _{B}^{B}+F_{A}\delta _{B}^{A}$

Comparación de casos

Como se ha dicho, la linealidad del problema exige que el trabajo total del caso 1 sea igual al total del caso 2. Igualando ambas expresiones y simplificando:

$F_{A}\delta _{B}^{A}=F_{B}\delta _{A}^{B}$

Que es un caso simplificado del teorema de Maxwell-Betti ya presentado, cuando los conjuntos de cargas $P_{i}\,$ y $Q_{j}\,$están constituidos, cada uno, por una única carga. La demostración del caso general se puede así abordar de forma sencilla por simple inducción a partir de lo explicado en este apartado.

Casos particulares

Teorema de Maxwell

Previamente al teorema de Maxwell-Betti, en 1864, James Clerk Maxwell publicó un teorema denominado "Método de las Distorsiones o Desplazamientos Recíprocos", al que contribuyeron notablemente los trabajos de otros científicos como Mohr y Clapeyron. Se considera que este teorema da lugar al primer método de análisis para estructuras estáticamente indeterminadas. Se enuncia como sigue:

Si sobre un cuerpo elástico actúa una causa en un punto A, la deformación que se produce en otro punto del sistema B es igual a la que se produciría en A si la causa actuase en B . J. C. Maxwell

Como vemos, este teorema no es sino un caso particular del general, expresado mediante el Teorema de Maxwell-Betti, puesto que aquí únicamente se considera la actuación de una fuerza y no un conjunto de ellas.

Simetría de la matriz de rigidez

El teorema de Maxwell-Betti aplicado a una estructura lineal caracterizable mediante una matriz de rigidez, implica que la matriz de rigidez debe ser simétrica. Ya que de no serlo el estado elástico final no sería único y dependería del orden y modo de aplicación de las cargas, lo cual contradice el carácter lineal de la estructura.

Véase también

• Resistencia de materiales
• Teoremas de Castigliano

Bibliografía

• Ortiz Berrocal, L., Resistencia de materiales, McGraw-Hill, 2002, ISBN 84-481-3353-6.
• Celigüeta, J.T., Curso de análisis estructural, Eunsa S.A, 1998, ISBN 978-8431316129.
• Becker, A.A., The Boundary Element Method in Engineering: A Complete Course, McGraw-Hill, 1992, ISBN 978-0077074395.
• Timoshenko, S., Resistencia de materiales. Teoría elemental y problemas, Espasa-Calpe, 1970, ISBN 84-239-6314-4.

• Datos: Q794269